好耐冇见了
时间:2014-01-21
来源:互联网
 (((自从上次果次之后一直冇研究....呢两日又无聊写下
(((自从上次果次之后一直冇研究....呢两日又无聊写下
multiarray<arg_type, Rank, Allocator> &Convolution(const multiarray<arg_type, Rank, Allocator> &signal,
const multiarray<arg_type, Rank, Allocator> &kernel, multiarray<arg_type, Rank, Allocator> &result)
{
__if_exists(arg_type::value_type)
{
typedef arg_type::value_type type;
}
__if_not_exists(arg_type::value_type)
{
typedef arg_type type;
}
size_t size[Rank], bound[Rank];
for(size_t i = 0; i < Rank; ++i)
{
size[i] = signal.size(i) + kernel.size(i) - 1;
bound[i] = std::max(signal.size(i), kernel.size(i));
bound[i] = 2 * (bound[i] + bound[i] % 2);
}
multiarray<arg_type, Rank, Allocator> a(signal), b(kernel);
a.resize(bound, (arg_type)0);
b.resize(bound, (arg_type)0);
auto fa(FourierTransform<type>(a)), fb(FourierTransform<type>(b));
std::transform(fa.begin(), fa.end(), fb.begin(), fa.begin(), std::multiplies<std::complex<type>>());
FourierTransform<type>(fa, fa);
__if_exists(arg_type::value_type)
{
InverseFourier(fa, a);
}
__if_not_exists(arg_type::value_type)
{
for(size_t i = 0; i < fa.size(); ++i)
a.at(i) = real(fa.at(i));
InverseFourier(a, a);
}
a.resize(size);
result.reshape(size);
std::copy(a.begin(), a.end(), result.begin());
return result;
}
template <typename type, typename arg_type, size_t Rank>
multiarray<std::complex<type>, Rank> &ParallelFourierTransform(const multiarray<arg_type, Rank> &buffer,
multiarray<std::complex<type>, Rank> &result)
{
size_t size = buffer.size(0);
result._base::reshape(buffer.shape().begin(),
(multiarray<arg_type, Rank>::pointer)nullptr, (multiarray<arg_type, Rank>::pointer)nullptr);
parallel_for(size, [&](size_t idx) -> void
{
multiarray<std::complex<type>, Rank - 1> row;
FourierTransform<type, arg_type, Rank - 1>(buffer[idx], row);
std::copy(row.begin(), row.end(), result[idx].begin());
});
return result;
}
template <typename type, typename arg_type>
multiarray<std::complex<type>> &CooleyTukey(const multiarray<arg_type> &buffer, const size_t radix, multiarray<std::complex<type>> &result)
{
const size_t N = buffer.size(), index[2][2] = {{radix, N / radix}, {N / radix, radix}};
const std::complex<type> TwiddleFactor = std::polar<type>(1, (type)-2 * (type)M_PI / (type)N);
multiarray<arg_type, 2> temp(index[1], buffer.begin(), buffer.end());
Transpose(temp, temp)._base::reshape(index[0], (multiarray<arg_type, 2>::pointer)nullptr, (multiarray<arg_type, 2>::pointer)nullptr);
multiarray<std::complex<type>, 2> reorder;
Transpose(ParallelFourierTransform<type>(temp, reorder), reorder);
for(size_t i = 0; i < reorder.size(0); ++i)
for(size_t j = 0; j < reorder.size(1); ++j)
reorder[i][j] *= std::pow<type>(TwiddleFactor, (type)i * (type)j);
Transpose(ParallelFourierTransform<type>(reorder, reorder), reorder);
result.reshape(N);
std::copy(reorder.begin(), reorder.end(), result.begin());
return result;
}
template <typename type, typename arg_type>
multiarray<std::complex<type>> &Bluestein(const multiarray<arg_type> &buffer, multiarray<std::complex<type>> &result)
{
const size_t N = buffer.size();
multiarray<std::complex<type>> signal(N), kernel(N), phase(N), temp;
for(size_t i = 0; i < N; ++i)
{
phase[i] = std::polar<double>(1, -(double)i * (double)i * (double)M_PI / (double)N);
kernel[i] = std::conj(phase[i]);
signal[i] = buffer[i] * phase[i];
}
Convolution(signal, kernel, temp);
if(N % 2)
std::transform(temp.begin(), temp.begin() + N - 1, temp.begin() + N, temp.begin(), std::minus<std::complex<double>>());
else
std::transform(temp.begin(), temp.begin() + N - 1, temp.begin() + N, temp.begin(), std::plus<std::complex<double>>());
result.reshape(N);
std::transform(phase.begin(), phase.end(), temp.begin(), result.begin(), std::multiplies<std::complex<type>>());
return result;
}
template <typename type, typename arg_type, size_t Rank>
multiarray<std::complex<type>, Rank> &FourierTransform(const multiarray<arg_type, Rank> &buffer, multiarray<std::complex<type>, Rank> &result)
{
typedef multiarray<type, Rank>::base_array base_array;
__if_exists(base_array::type)
{
const size_t index[2] = {buffer.size(0), buffer.size(0, 2)};
multiarray<std::complex<type>, 2> reorder(index[0], index[1]);
multiarray<std::complex<type>, Rank> rows;
ParallelFourierTransform<type, arg_type, Rank>(buffer, rows);
std::copy(rows.begin(), rows.end(), reorder.begin());
Transpose(reorder, reorder);
ParallelFourierTransform<type, std::complex<type>>(reorder, reorder);
Transpose(reorder, reorder);
for(size_t i = 0; i < Rank; ++i)
result.reshape(i + 1, buffer.size(i));
std::copy(reorder.begin(), reorder.end(), result.begin());
}
__if_not_exists(base_array::type)
{
const size_t N = buffer.size();
switch(N)
{
case 0:
break;
case 1:
result.reshape(N);
result[0] = buffer[0];
break;
case 2:
{
arg_type temp[] = {buffer[0], buffer[1]};
result.reshape(N);
result[0] = temp[0] + temp[1];
result[1] = temp[0] - temp[1];
}
break;
default:
{
if(GCD(N, 2) != 1)
{
if(!(N % 2))
CooleyTukey<type>(buffer, 2, result);
else if(!(N % 3))
CooleyTukey<type>(buffer, 3, result);
else if(!(N % 5))
CooleyTukey<type>(buffer, 5, result);
else
CooleyTukey<type>(buffer, 7, result);
break;
}
auto radix = (*Decompose(N).begin()).first;
if(radix < N)
{
CooleyTukey<type>(buffer, (size_t)radix, result);
break;
}
Bluestein<type>(buffer, result);
}
break;
}
}
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &InverseFourier(const multiarray<type, Rank, Allocator> &buffer,
multiarray<type, Rank, Allocator> &result)
{
using namespace std::placeholders;
typedef multiarray<type, Rank, Allocator>::base_array base_array;
size_t size = buffer.size(0);
result._base::reshape(buffer.shape().begin(),
(multiarray<type, Rank, Allocator>::pointer)nullptr, (multiarray<type, Rank, Allocator>::pointer)nullptr);
__if_exists(base_array::type)
{
multiarray<type, Rank, Allocator> temp(buffer);
parallel_for(size, [&](size_t idx) -> void
{
multiarray<type, Rank - 1, Allocator> row;
InverseFourier<type, Rank - 1, Allocator>(buffer[(size - idx) % size], row);
std::copy(row.begin(), row.end(), temp[idx].begin());
});
std::transform(temp.begin(), temp.end(), result.begin(), std::bind(std::divides<type>(), _1, size));
}
__if_not_exists(base_array::type)
{
std::transform(buffer.begin(), buffer.end(), result.begin(), std::bind(std::divides<type>(), _1, size));
std::reverse(result.begin() + 1, result.end());
}
return result;
}
作者: Susan﹏汪汪 发布时间: 2014-01-21
作者: a8d7e8 发布时间: 2014-01-21
你识唔识写 STFT 呀汪汪?
再计算FFT就是
作者: Susan﹏汪汪 发布时间: 2014-01-21
点样可以找到最细的2,3,5,7的power
谂住hard code写2,3,5,7的FFT
然后做convolution时就可以再减少运算
作者: Susan﹏汪汪 发布时间: 2014-01-21
2,3,5,7 是甚么单位啊?
power 是指 exponential power? (eg. 2^a, 3^b ?? 还是 a^2, b^3....)
汪汪想问
点样可以找到最细的2,3,5,7的power
谂住hard code写2,3,5,7的FFT
然后做convolution时就可以再减少运算
作者: a8d7e8 发布时间: 2014-01-21
唔明哦.......
2,3,5,7 是甚么单位啊?
power 是指 exponential power? (eg. 2^a, 3^b ?? 还是 a^2, b^3....)
即例如17
最近的最小倍数是2*3*3=18
咁就可以分解成radix-2的CooleyTukey和radix-3的CooleyTukey
作者: Susan﹏汪汪 发布时间: 2014-01-21
除得唔得架?
2,3,5,7的倍数
即例如17
最近的最小倍数是2*3*3=18
咁就可以分解成radix-2的CooleyTukey和radix-3的CooleyTukey
作者: a8d7e8 发布时间: 2014-01-21
例如一个length 17的signal
做convolution的话会得出length 33的output
所以就做zero pudding至最近的5*7=35
就可以做radix-5 CooleyTukey or radix-7 CooleyTukey
[ 本帖最后由 Susan﹏汪汪 於 2013-12-13 01:57 PM 使用 编辑 ]
作者: Susan﹏汪汪 发布时间: 2014-01-21
果然系一个好好的 idea!
Given n, find the nearest number m where n <= m such that m is a composite number with factors only in the set of 2, 3, 5 and 7.
Alternately, if the cost of zero padding is much lower than to find the nearest m_k where m_(k+1) < m_(k), that is:
cost(finding nearest m_k) + cost(zero padding m_k-n) < cost(finding nearest m)
Then it should be acceptable to use m_(k) as the solution.
因为要做zero pudding嘛
例如一个length 17的signal
做convolution的话会得出length 33的output
所以就做zero pudding至最近的5*7=35
就可以做radix-5 CooleyTukey or radix-7 CooleyTukey
作者: a8d7e8 发布时间: 2014-01-21
看了一轮 wiki, 明白你的用意了.
果然系一个好好的 idea!
Given n, find the nearest number m where n
[ 本帖最后由 Susan﹏汪汪 於 2013-12-13 03:18 PM 使用 编辑 ]
作者: Susan﹏汪汪 发布时间: 2014-01-21
struct complex_type
{
typedef typename std::conditional<std::is_arithmetic<arg_type>::value, std::complex<arg_type>, arg_type>::type::value_type value_type;
typedef std::complex<value_type> type;
};
#define _COMPLEX_TYPE typename complex_type<arg_type>::type
#define _COMPLEX_ALLOC_TYPE typename std::allocator_traits<Allocator>::template rebind_alloc<_COMPLEX_TYPE>::other
template <typename arg_type, size_t Rank, typename Allocator>
multiarray<arg_type, Rank, Allocator> &Convolution(const multiarray<arg_type, Rank, Allocator> &signal,
const multiarray<arg_type, Rank, Allocator> &kernel, multiarray<arg_type, Rank, Allocator> &result)
{
typedef std::conditional<std::is_arithmetic<arg_type>::value, std::complex<arg_type>, arg_type>::type::value_type type;
typedef std::complex<type> complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t size[Rank], bound[Rank];
for(size_t i = 0; i < Rank; ++i)
{
size[i] = signal.size(i) + kernel.size(i) - 1;
bound[i] = size[i] + signal.size(i) % 2 + kernel.size(i) % 2 + 1;
}
multiarray<arg_type, Rank, Allocator> a(signal), b(kernel);
a.resize(bound, (arg_type)0);
b.resize(bound, (arg_type)0);
multiarray<complex_type, Rank, complex_alloc_type> temp;
FourierTransform(PointwiseProduct(FourierTransform(a), FourierTransform(b)), temp);
__if_exists(arg_type::value_type)
{
InverseFourier(temp, a);
}
__if_not_exists(arg_type::value_type)
{
for(size_t i = 0; i < temp.size(); ++i)
a.at(i) = real(temp.at(i));
InverseFourier(a, a);
}
a.resize(size);
result.reshape(size);
std::copy(a.begin(), a.end(), result.begin());
return result;
}
template <typename arg_type, size_t Rank, typename Allocator>
multiarray<_COMPLEX_TYPE, Rank, _COMPLEX_ALLOC_TYPE> &ParallelFourierTransform(const multiarray<arg_type, Rank, Allocator> &buffer,
multiarray<_COMPLEX_TYPE, Rank, _COMPLEX_ALLOC_TYPE> &result)
{
typedef std::conditional<std::is_arithmetic<arg_type>::value, std::complex<arg_type>, arg_type>::type::value_type type;
typedef std::complex<type> complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t size = buffer.size(0);
result._base::reshape(buffer.shape().begin(),
(multiarray<arg_type, Rank>::pointer)nullptr, (multiarray<arg_type, Rank>::pointer)nullptr);
parallel_for(size, [&](size_t idx) -> void
{
multiarray<complex_type, Rank - 1, complex_alloc_type> row;
FourierTransform<arg_type, Rank - 1, Allocator>(buffer[idx], row);
std::copy(row.begin(), row.end(), result[idx].begin());
});
return result;
}
template <typename arg_type, typename Allocator>
multiarray<_COMPLEX_TYPE, 1, _COMPLEX_ALLOC_TYPE> &CooleyTukey(const multiarray<arg_type, 1, Allocator> &buffer, const size_t radix,
multiarray<_COMPLEX_TYPE, 1, _COMPLEX_ALLOC_TYPE> &result)
{
typedef std::conditional<std::is_arithmetic<arg_type>::value, std::complex<arg_type>, arg_type>::type::value_type type;
typedef std::complex<type> complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
const size_t N = buffer.size(), index[2][2] = {{radix, N / radix}, {N / radix, radix}};
const complex_type TwiddleFactor = std::polar<type>(1, (type)-2 * (type)M_PI / (type)N);
multiarray<arg_type, 2, Allocator> temp(index[1], buffer.begin(), buffer.end());
Transpose(temp, temp)._base::reshape(index[0],
(multiarray<arg_type, 2, Allocator>::pointer)nullptr, (multiarray<arg_type, 2, Allocator>::pointer)nullptr);
multiarray<complex_type, 2, complex_alloc_type> reorder;
Transpose(ParallelFourierTransform(temp, reorder), reorder);
for(size_t i = 0; i < reorder.size(0); ++i)
for(size_t j = 0; j < reorder.size(1); ++j)
reorder[i][j] *= std::pow<type>(TwiddleFactor, (type)i * (type)j);
Transpose(ParallelFourierTransform(reorder, reorder), reorder);
result.reshape(N);
std::copy(reorder.begin(), reorder.end(), result.begin());
return result;
}
template <typename arg_type, typename Allocator>
multiarray<_COMPLEX_TYPE, 1, _COMPLEX_ALLOC_TYPE> &Bluestein(const multiarray<arg_type, 1, Allocator> &buffer,
multiarray<_COMPLEX_TYPE, 1, _COMPLEX_ALLOC_TYPE> &result)
{
typedef std::conditional<std::is_arithmetic<arg_type>::value, std::complex<arg_type>, arg_type>::type::value_type type;
typedef std::complex<type> complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
const size_t N = buffer.size();
const complex_type TwiddleFactor = std::polar<type>(1, (type)-2 * (type)M_PI / (type)N);
multiarray<complex_type, 1, complex_alloc_type> signal(N), kernel(N), phase(N), temp;
for(size_t i = 0; i < N; ++i)
{
phase[i] = std::pow<type>(TwiddleFactor, (type)i * (type)i / 2);
kernel[i] = std::conj(phase[i]);
signal[i] = buffer[i] * phase[i];
}
Convolution(signal, kernel, temp);
if(N % 2)
std::transform(temp.begin(), temp.begin() + N - 1, temp.begin() + N, temp.begin(), std::minus<complex_type>());
else
std::transform(temp.begin(), temp.begin() + N - 1, temp.begin() + N, temp.begin(), std::plus<complex_type>());
result.reshape(N);
std::transform(phase.begin(), phase.end(), temp.begin(), result.begin(), std::multiplies<complex_type>());
return result;
}
template <typename arg_type, size_t Rank, typename Allocator>
multiarray<_COMPLEX_TYPE, Rank, _COMPLEX_ALLOC_TYPE> &FourierTransform(const multiarray<arg_type, Rank, Allocator> &buffer,
multiarray<_COMPLEX_TYPE, Rank, _COMPLEX_ALLOC_TYPE> &result)
{
typedef std::conditional<std::is_arithmetic<arg_type>::value, std::complex<arg_type>, arg_type>::type::value_type type;
typedef std::complex<type> complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
typedef multiarray<arg_type, Rank, Allocator>::base_array base_array;
__if_exists(base_array::type)
{
const size_t index[2] = {buffer.size(0), buffer.size(0, 2)};
multiarray<complex_type, 2, complex_alloc_type> reorder(index[0], index[1]);
multiarray<complex_type, Rank, complex_alloc_type> rows;
ParallelFourierTransform(buffer, rows);
std::copy(rows.begin(), rows.end(), reorder.begin());
Transpose(reorder, reorder);
ParallelFourierTransform(reorder, reorder);
Transpose(reorder, reorder);
for(size_t i = 0; i < Rank; ++i)
result.reshape(i + 1, buffer.size(i));
std::copy(reorder.begin(), reorder.end(), result.begin());
}
__if_not_exists(base_array::type)
{
const size_t N = buffer.size();
switch(N)
{
case 0:
break;
case 1:
result.reshape(N);
result[0] = buffer[0];
break;
case 2:
{
arg_type temp[] = {buffer[0], buffer[1]};
result.reshape(N);
result[0] = temp[0] + temp[1];
result[1] = temp[0] - temp[1];
}
break;
case 3:
{
arg_type temp[] = {buffer[0], buffer[1], buffer[2]};
const complex_type TwiddleFactor = std::polar<type>(1, (type)-2 * (type)M_PI / (type)N),
phase[] = {TwiddleFactor, std::conj(TwiddleFactor)};
result.reshape(N);
result[0] = temp[0] + temp[1] + temp[2];
result[1] = temp[0] + temp[1] * phase[0] + temp[2] * phase[1];
result[2] = temp[0] + temp[1] * phase[1] + temp[2] * phase[0];
}
break;
default:
{
if(GCD(N, 6) != 1)
{
if(!(N % 2))
CooleyTukey(buffer, 2, result);
else if(!(N % 3))
CooleyTukey(buffer, 3, result);
else if(!(N % 5))
CooleyTukey(buffer, 5, result);
else
CooleyTukey(buffer, 7, result);
break;
}
size_t radix = (size_t)Decompose(N).begin()->first;
if(radix < N)
{
CooleyTukey(buffer, radix, result);
break;
}
Bluestein(buffer, result);
}
break;
}
}
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &InverseFourier(const multiarray<type, Rank, Allocator> &buffer,
multiarray<type, Rank, Allocator> &result)
{
using namespace std::placeholders;
typedef multiarray<type, Rank, Allocator>::base_array base_array;
size_t size = buffer.size(0);
result._base::reshape(buffer.shape().begin(),
(multiarray<type, Rank, Allocator>::pointer)nullptr, (multiarray<type, Rank, Allocator>::pointer)nullptr);
__if_exists(base_array::type)
{
multiarray<type, Rank, Allocator> temp(buffer);
parallel_for(size, [&](size_t idx) -> void
{
multiarray<type, Rank - 1, Allocator> row;
InverseFourier<type, Rank - 1, Allocator>(buffer[(size - idx) % size], row);
std::copy(row.begin(), row.end(), temp[idx].begin());
});
std::transform(temp.begin(), temp.end(), result.begin(), std::bind(std::divides<type>(), _1, size));
}
__if_not_exists(base_array::type)
{
std::transform(buffer.begin(), buffer.end(), result.begin(), std::bind(std::divides<type>(), _1, size));
std::reverse(result.begin() + 1, result.end());
}
return result;
}
作者: Susan﹏汪汪 发布时间: 2014-01-21

太深奥啦,睇唔明...
有机会要读下 FFT,应用范围好大...
作者: fitcat07 发布时间: 2014-01-21
看了一轮 wiki, 明白你的用意了.
果然系一个好好的 idea!
Given n, find the nearest number m where n
不过只是加翻length-3, length-5, length-7的hard code
在计算length-44100时
原本只有length-2和length-3用了33秒时间计算
加了 length-5就变成20几秒时间
加了 length-7变成一闪间计算完
作者: Susan﹏汪汪 发布时间: 2014-01-21

其实我无深研 n-radix Cooley Tukey FFT, 所以唔肯定计 length-16 需要计几多次 length-2.
系咪都要计四次?
之所以快咗系咪因为 hard code 的 NRCTFFT 可简化好多?
即系计 length-44100 实际上要做八次 NRCTFFT?
事关对住 FFT 条式我已投降咗一半. 当中的原理和输入输出好似明咗但好快又忘记了...
超正.....汪汪仲未研究到如何找出最细的(2, 3, 5, 7)的倍数
不过只是加翻length-3, length-5, length-7的hard code
在计算length-44100时
原本只有length-2和length-3用了33秒时间计算
加了 length-5就变成20几 ...
作者: a8d7e8 发布时间: 2014-01-21

其实我无深研 n-radix Cooley Tukey FFT, 所以唔肯定计 length-16 需要计几多次 length-2.
系咪都要计四次?
之所以快咗系咪因为 hard code 的 NRCTFFT 可简化好多?
即系计 length-44 ...
Length-7的要转成length-16的来做convolution
作者: Susan﹏汪汪 发布时间: 2014-01-21

其实我无深研 n-radix Cooley Tukey FFT, 所以唔肯定计 length-16 需要计几多次 length-2.
系咪都要计四次?
之所以快咗系咪因为 hard code 的 NRCTFFT 可简化好多?
即系计 length-44 ...
Length-16有4次length-2 FFT
44100=49*9*100
=7^2 * 3^2 * 5^2 * 2^2
即有3次Cooley Tukey (8次FFT)
[ 本帖最后由 Susan﹏汪汪 於 2013-12-15 01:45 PM 使用 编辑 ]
作者: Susan﹏汪汪 发布时间: 2014-01-21
谂到方式可以更一般化N维signal的运算
因为把DFT转成DCT的话
发现不能直接用N维DFT转N维DCT
作者: Susan﹏汪汪 发布时间: 2014-01-21
今晚又要大改段code
谂到方式可以更一般化N维signal的运算
因为把DFT转成DCT的话
发现不能直接用N维DFT转N维DCT
那么以下算法也可以计算得到 FFT:
一:把 k = 非 2^n 个 time domain sample 用 spline interpolation 转成 2^n 个 sample,然后
二:把 2^n 个 sample 做 FFT
三:把 2^n 个 frequency domain FFT 结果(complex number)再用 spline interpolation 转成 k 个 FFT 结果
还可以考虑要求的准确度是大还是小来选择 2^n 是要大过 k 还是小过 k 呢!
或许这个算法不会是最快,但若以 big-O notation 来看时间的话,应该不算慢。
作者: xianrenb 发布时间: 2014-01-21
如果无理解错的话,即是你的算法是容许计算上一定的误差。
那么以下算法也可以计算得到 FFT:
一:把 k = 非 2^n 个 time domain sample 用 spline interpolation 转成 2^n 个 sample,然后
二:把 2^n 个 sa ...
跟Wikipedia的说法应该会比直接计算DFT更准确
因为Cooley Tukey比直接计算花更少乘法和加法
Floating point error会更小
不过汪汪有试过同时直接运算和fft比较
的确会有差误差
[ 本帖最后由 Susan﹏汪汪 於 2013-12-16 03:01 PM 使用 编辑 ]
作者: Susan﹏汪汪 发布时间: 2014-01-21
作者: a8d7e8 发布时间: 2014-01-21
如果无理解错的话,即是你的算法是容许计算上一定的误差。
那么以下算法也可以计算得到 FFT:
一:把 k = 非 2^n 个 time domain sample 用 spline interpolation 转成 2^n 个 sample,然后
二:把 2^n 个 sa ...
如果是把sample缩小的话误差会好大
如果是放大sample
做zero pudding仲实际
一来做convolution时. 任意Zero pudding是不影响结果(只是有floating error)
Bluestein fft就是使用这特性
作者: Susan﹏汪汪 发布时间: 2014-01-21
系喎差啲唔记得你都用过 FFT 做 stock analysis!
详细就不便说了。
作者: xianrenb 发布时间: 2014-01-21
不过如果按照你的算法
如果是把sample缩小的话误差会好大
如果是放大sample
做zero pudding仲实际
一来做convolution时. 任意Zero pudding是不影响结果(只是有floating error)
Bluestein fft就是使用这特性
...
事实上如果是在电路仿真软件(SPICE)上应用的话,一般情况下都是选用 2^n 个 sample 的 FFT 。
但取 time domain 的 sample 时应该就是做了某种 interpolation ,因为仿真结果都是一段段的讯号大小变化而已。
可以说 sample 的时间位置基本上是对不到 simulation 的结果的。
得出的 FFT 图表,人们很多时亦用来找“对不正的” frequency 的结果。
软件亦应是利用 interpolation 才能画出。
换言之,一般人使用电路仿真软件来做 FFT 的话,其实都已用上了我所述的方法。
作者: xianrenb 发布时间: 2014-01-21
我估我的算法误差不一定大,因为先后都要做 interpolation 。
事实上如果是在电路仿真软件(SPICE)上应用的话,一般情况下都是选用 2^n 个 sample 的 FFT 。
但取 time domain 的 sample 时应该就是做了某种 in ...
如果缩小sample系咪会失去高频信号..??
作者: Susan﹏汪汪 发布时间: 2014-01-21
喔..??
如果缩小sample系咪会失去高频信号..??
但如果是正常的电子讯号或现实数据,做了 interpolation 后应该就不会有太大差别。
即是说第二次 interpolation 可以“大概估到”失去了的 data 是什么。
而且,若第一次 interpolation 是选用增加 sample 数目的方法的话,我看应该是没有资料减少的情况。
P.S. 如果我没搞错,取 N 个 sample 是占 T 那么长的时间的话, FFT 得出的结果所对应的最高 frequency 为 (N-1)/T 。
[ 本帖最后由 xianrenb 於 2013-12-18 08:57 AM 编辑 ]
作者: xianrenb 发布时间: 2014-01-21
想了一会都不明白,后来看过:
http://stackoverflow.com/questions/4364823/how-to-get-frequency-from-fft-result
So if your sample rate, Fs is say 44.1 kHz and your FFT size, N is 1024, then the FFT output bins are at:
0: 0 * 44100 / 1024 = 0.0 Hz
1: 1 * 44100 / 1024 = 43.1 Hz
2: 2 * 44100 / 1024 = 86.1 Hz
3: 3 * 44100 / 1024 = 129.2 Hz
4: ...
5: ...
...
511: 511 * 44100 / 1024 = 22006.9 Hz
Note that for a real input signal (imaginary parts all zero) the second half of the FFT (bins from N / 2 + 1 to N - 1) contain no useful additional information (they have complex conjugate symmetry with the first N / 2 - 1 bins). The last useful bin (for practical aplications) is at N / 2 - 1, which corresponds to 22006.9 Hz in the above example. The bin at N / 2 represents energy at the Nyquist frequency, i.e. Fs / 2 ( = 22050 Hz in this example), but this is in general not of any practical use, since anti-aliasing filters will typically attenuate any signals at and above Fs / 2.
换言之,不必太介意高频讯号计 FFT 算得是否准确,因为本来 sampling 就已经做不准高频部份。
这是 sampling 本身的限制。
作者: xianrenb 发布时间: 2014-01-21
我发现了 LTspice 中的 FFT 把 10 ms 的 simulation result 以 8 个 sample 、不做 smoothing 来做 FFT 的话是出 100 Hz ~ 300 Hz 的图的。
想了一会都不明白,后来看过:
http://stackoverflow.com/questions/436 ...
即是44100 length的sample
最高frequency只去到22050
之后的都会是重覆
所以FFT的计算结果
中间的才是高频
[ 本帖最后由 Susan﹏汪汪 於 2013-12-18 01:55 PM 使用 编辑 ]
作者: Susan﹏汪汪 发布时间: 2014-01-21
Hard code果到都可以唔洗计算后半段的FFT
作者: Susan﹏汪汪 发布时间: 2014-01-21
sample 数目小了,就一定有些资料会失去,因为计 degree of freedom 是小了嘛。
但如果是正常的电子讯号或现实数据,做了 interpolation 后应该就不会有太大差别。
即是说第二次 interpolation 可以“大概估到 ...
作者: form5 发布时间: 2014-01-21
sample 数目小了,就一定有些资料会失去,因为计 degree of freedom 是小了嘛。
但如果是正常的电子讯号或现实数据,做了 interpolation 后应该就不会有太大差别。
即是说第二次 interpolation 可以“大概估到 ...
有咩好的interpolation算法

作者: Susan﹏汪汪 发布时间: 2014-01-21
FFT的后半段都是前半段的conjugate
即是44100 length的sample
最高frequency只去到22050
之后的都会是重覆
所以FFT的计算结果
中间的才是高频
不过有点几得意,就是 FFT 后半段与前半段算法是一样的。
第一个 bin 是 DC 。
第二个 bin 是与 1 个 2 Pi 的数有关。
第 N 个 bin 是与 N - 1 个 2 Pi 的数有关。
所以我就想到最高 frequency 是 (N - 1) / T 了。
而如果只知道前半段与后半段“对称”,又怎知道是后半段错而不是前半段错呢?
只因我们知道 sampling 的 frequency 要高於结果的 frequency 一倍(即 double )才准确。
但“不准确”的后半部份 FFT 又是否 100% 完全错误、不能代表高频部份、无用呢?
我会有点保留。(可想想若问题是不用求完整的 FFT ,而只要求得 (N - 1) / T 这个 frequency / bin 的结果应该用什么数式?)
当然,如果应用要求是要高准确度的 frequency domain 结果的话,后半部份就不合用。
[ 本帖最后由 xianrenb 於 2013-12-19 06:28 PM 编辑 ]
作者: xianrenb 发布时间: 2014-01-21
另外想问
有咩好的interpolation算法

不过我未用过,怎样计算也不是太清楚。
另外,如果你的算法是把 N 个 sample 的 FFT 问题转成最近的 X * Y 个 sample 的 FFT 问题的话,为何不把单数个 sample 的 FFT 问题转成双数个 sample 的 FFT 问题呢?
这样的话 recursion 之下就好易解决。
作者: xianrenb 发布时间: 2014-01-21
其实我的数学不太好,而且学 FFT 已是很久前的事,基本上都忘掉了。
不过有点几得意,就是 FFT 后半段与前半段算法是一样的。
第一个 bin 是 DC 。
第二个 bin 是与 1 个 2 Pi 的数有关。
第 N 个 bin 是与 ...


作者: Susan﹏汪汪 发布时间: 2014-01-21
我估先前提过的 spline interpolation 应该不错。
不过我未用过,怎样计算也不是太清楚。
另外,如果你的算法是把 N 个 sample 的 FFT 问题转成最近的 X * Y 个 sample 的 FFT 问题的话,为何不把单数个 sampl ...
不过想再减少运算量
作者: Susan﹏汪汪 发布时间: 2014-01-21
原来对於complex signal
DFT后半段并不是前半段的conj
结果hard code部分还是不能化简
作者: Susan﹏汪汪 发布时间: 2014-01-21
我估先前提过的 spline interpolation 应该不错。
不过我未用过,怎样计算也不是太清楚。
另外,如果你的算法是把 N 个 sample 的 FFT 问题转成最近的 X * Y 个 sample 的 FFT 问题的话,为何不把单数个 sampl ...
作者: Susan﹏汪汪 发布时间: 2014-01-21
不太明白


但 (N - 1) / T 这个 bin 却是 FFT 的后半部份!
所以我会估 FFT 后半部份也许有点能代表高频部份,而不是 100% 全错。
作者: xianrenb 发布时间: 2014-01-21
其实我的数学不太好,而且学 FFT 已是很久前的事,基本上都忘掉了。
不过有点几得意,就是 FFT 后半段与前半段算法是一样的。
第一个 bin 是 DC 。
第二个 bin 是与 1 个 2 Pi 的数有关。
第 N 个 bin 是与 ...
第 n 个 bin 是 N 个 term 相加。
每个 term 都可用 sin 、 cos 求得。
第一个 term 与 0 / N * (n - 1) * 2 Pi 有关。
第二个 term 与 1 / N * (n - 1) * 2 Pi 有关。
第 k 个 term 与 (k-1) / N * (n - 1) * 2 Pi 有关。
即是 N 个 term 的变化由 0 * (n - 1) * 2 Pi 至 大约 1 * (n - 1) * 2 Pi 有关。
我的理解是,第 n 个 bin 的结果,是原来的 data ,与 wave length 为 T / (n - 1) 的 sin 、 cos 等 wave 有几相似。
T 是指 N 个 time domain sample 所占的总时间。
作者: xianrenb 发布时间: 2014-01-21
即是说,如果给了 time domain 中的 N 个 sample data ,若要求 frequency domain 中的 (N - 1) / T 对应的数值是什么的话,即使未学过 FFT ,求得的算式应该就与 FFT 中最后一个 bin 的数式相同。
但 (N - 1) ...
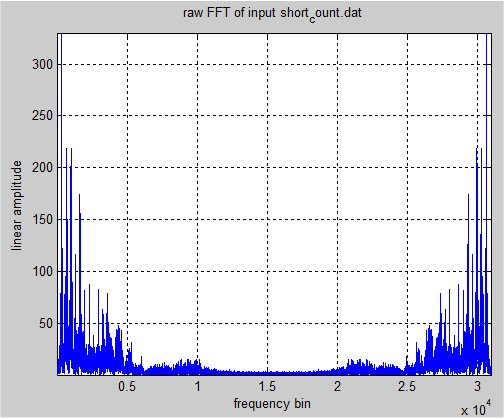
DFT后半部是前半部分的Conj
DFT没有资料放大的特性
原本的N*sizeof(float)的资料
变成N*sizeof(complex)的资料
所以就有N/2的资料是重复
也所以、最高频只有N/2
作者: Susan﹏汪汪 发布时间: 2014-01-21
作者: Susan﹏汪汪 发布时间: 2014-01-21
没理由与 FFT 中最后一个 bin 不一样吧?
当然,大家都知那是错误的结果,但那却是最接近正确答案的结果。
...
作者: xianrenb 发布时间: 2014-01-21
不是
DFT后半部是前半部分的Conj
DFT没有资料放大的特性
原本的N*sizeof(float)的资料
变成N*sizeof(complex)的资料
所以就有N/2的资料是重复
也所以、最高频只有N/2
http://i.discuss.com.hk/d/images/r ...
没理由与 FFT 中最后一个 bin 不一样吧?
当然,大家都知那是错误的结果,但那却是最接近正确答案的结果。
另外,你用的应该是 [url=http://en.wikipedia.org/wiki/Bluestein's_FFT_algorithm]http://en.wikipedia.org/wiki/Bluestein's_FFT_algorithm[/url] 中的方法。
如果说 sample rate 是 1 Hz ,即是 wave length 是 1 s 。
那么 17 个 sample 就是头尾相差 16 s ,做 FFT 出 17 个 bin ,frequency 就是 0 、 1 / 17s 、 2 / 17 s ……。
35 个 sample 就是头尾相差 34 s ,做 FFT 出 35 个 bin , frequency 就是 0 、 1 / 35s 、 2 / 35s ……。
按理这 35 个 bin 之后怎样做 convolution ,都出不到对应 17 个 bin 的 frequency ?
作者: xianrenb 发布时间: 2014-01-21
如当 n <= 16 ,直接计算 DFT 。
当 n > 16 并且是单数的话,用 interpolation 把 sample size 加大至 n + 1 个 sample , FFT 后把 n + 1 个 bin 用 interpolation 减至 n 个 bin 。
若 n > 16 并且是双数的话,用普通 FFT 解决方法,把问题的 size 分至 n / 2 。
作者: xianrenb 发布时间: 2014-01-21
如果不是的话,那么你算出的 (N-1)/ T 那个 frequency domain 结果应是什么算式?
没理由与 FFT 中最后一个 bin 不一样吧?
当然,大家都知那是错误的结果,但那却是最接近正确答案的结果。
另外,你用的应 ...
慢慢来解释
Bluestein算法那个
其实是在数学上证明了zero pudding后的data再做convolution
是等价於直接运算
而Bluestein只是重新组合过数式
变成convolution
所以计算结果也是等价於DFT
类似的正如Cooley Tukey一样
只是数学游戏
比如说
以下两个sample
7 5 2
9 4 6
直接运算得出的convolution会是: 63 73 80 38 12
如果使用FFT的话
得出的是: 101 85 80
如果做zero pudding
变成
7 5 2 0
9 4 6 0
FFT算出: 75 73 80 38
如果是
7 5 2 0 0
9 4 6 0 0
FFT算出: 63 73 80 38 12
如果是
7 5 2 0 0 0
9 4 6 0 0 0
FFT算出: 63 73 80 38 12 0
这是因为FFT算出的convolution系circular
Zero pudding 是用来消除这个效果
作者: Susan﹏汪汪 发布时间: 2014-01-21
等等先
慢慢来解释
Bluestein算法那个
其实是在数学上证明了zero pudding后的data再做convolution
是等价於直接运算
而Bluestein只是重新组合过数式
变成convolution
所以计算结果也是等价於DFT
类似的正如Coo ...
我们知道如果相距 1 s 的 time-domain signal 做 convolution 后,对应的时间还是相距 1 s 。
那么相距 1 Hz 的 frequency-domain signal 做 convolution 后,对应的 frequency 也应该是相距 1 Hz 吧?
作者: xianrenb 发布时间: 2014-01-21
热门阅读
-
 office 2019专业增强版最新2021版激活秘钥/序列号/激活码推荐 附激活工具
office 2019专业增强版最新2021版激活秘钥/序列号/激活码推荐 附激活工具
阅读:74
-
 如何安装mysql8.0
如何安装mysql8.0
阅读:31
-
 Word快速设置标题样式步骤详解
Word快速设置标题样式步骤详解
阅读:28
-
 20+道必知必会的Vue面试题(附答案解析)
20+道必知必会的Vue面试题(附答案解析)
阅读:37
-
 HTML如何制作表单
HTML如何制作表单
阅读:22
-
 百词斩可以改天数吗?当然可以,4个步骤轻松修改天数!
百词斩可以改天数吗?当然可以,4个步骤轻松修改天数!
阅读:31
-
 ET文件格式和XLS格式文件之间如何转化?
ET文件格式和XLS格式文件之间如何转化?
阅读:24
-
 react和vue的区别及优缺点是什么
react和vue的区别及优缺点是什么
阅读:121
-
 支付宝人脸识别如何关闭?
支付宝人脸识别如何关闭?
阅读:21
-
 腾讯微云怎么修改照片或视频备份路径?
腾讯微云怎么修改照片或视频备份路径?
阅读:28















