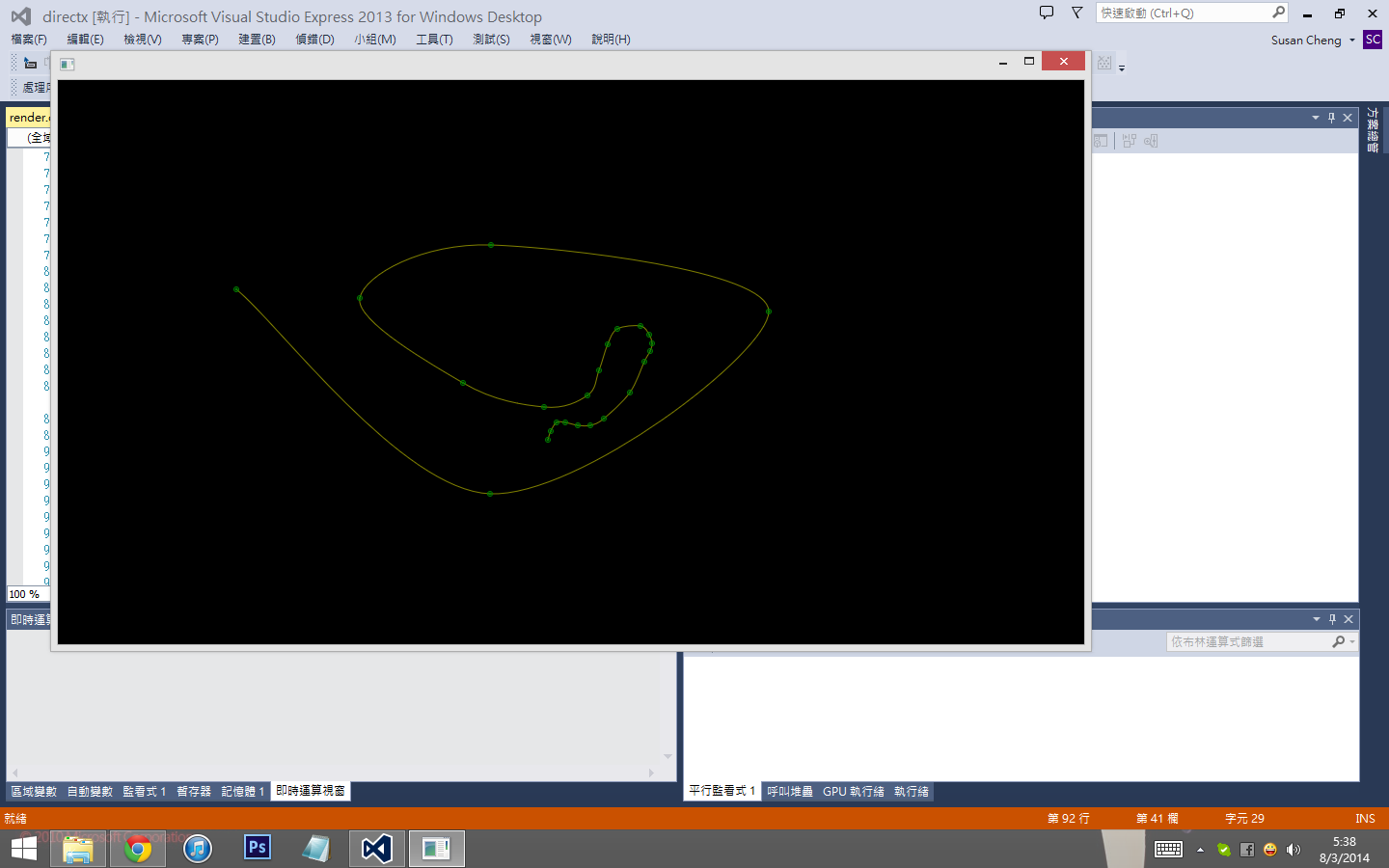
interpolation
时间:2014-03-20
来源:互联网
作者: Susan﹏汪汪 发布时间: 2014-03-20
系 spline interpolation?定用 Bezier curves 做?
作者: fitcat07 发布时间: 2014-03-20
引用:原帖由 fitcat07 於 2014-3-9 09:28 AM 发表
系 spline interpolation?定用 Bezier curves 做?
Cubic Hermite spline可以转换成Bézier curve 系 spline interpolation?定用 Bezier curves 做?
作者: Susan﹏汪汪 发布时间: 2014-03-20
复制内容到剪贴板代码:template <typename type>
type PointToBezier(const multiarray<vector<type>> &bezier, const vector<type> &point)
{
multiarray<vector<type>> _bezier = BezierDerivative(bezier), _bezier2 = BezierDerivative(_bezier);
auto getInterval = [](const type x) -> type
{
if(x < 0)
return 0;
if(x > 1)
return 1;
return x;
};
auto _NewtonsMethod = [&](type x)
{
x = getInterval(x);
//**********Newton's method
vector<type> d = BezierPoint<type>(bezier, x) - point, _d = BezierPoint<type>(_bezier, x);
x -= Dot(d, _d) / (Dot(d, BezierPoint<type>(_bezier2, x)) + Dot(_d, _d));
return x;
};
auto _Correction = [&](type x) -> type
{
x = getInterval(x);
//**********Correction
type head = Norm(point - bezier.front()),
middle = Norm(point - BezierPoint<type>(bezier, x)),
end = Norm(point - bezier.back());
if(middle > head && head < end)
x = 0;
if(middle > end && head > end)
x = 1;
return x;
};
return _Correction(_NewtonsMethod(_NewtonsMethod(0.5)));
}
template <typename type>
multiarray<vector<type>> &BezierIntersection(const multiarray<vector<type>> &bezier1,
const multiarray<vector<type>> &bezier2, multiarray<vector<type>> &result = multiarray<vector<type>>())
{
multiarray<vector<type>> _bezier1 = BezierDerivative(bezier1), _bezier2 = BezierDerivative(bezier2);
auto getInterval = [](const type x) -> type
{
if (x < 0)
return 0;
if (x > 1)
return 1;
return x;
};
auto _NewtonsMethod = [&](type &x, type &y)
{
x = getInterval(x);
y = getInterval(y);
//**********Newton's method
vector<type> d = BezierPoint<type>(bezier1, x) - BezierPoint<type>(bezier2, y),
_dx = BezierPoint<type>(_bezier1, x), _dy = -BezierPoint<type>(_bezier2, y);
type det = _dx[0] * _dy[1] - _dy[0] * _dx[1];
x -= (_dy[1] * d[0] - _dy[0] * d[1]) / det;
y -= (_dx[0] * d[1] - _dx[1] * d[0]) / det;
};
result.clear();
for (type i = 0; i <= 1; i += (type)1 / ((bezier1.size() - 1) * (bezier2.size() - 1)))
{
type x = PointToBezier(bezier1, BezierPoint(bezier2, i)), y = i;
_NewtonsMethod(x, y);
_NewtonsMethod(x, y);
if (x >= 0 && x <= 1 && y >= 0 && y <= 1
&& Norm(BezierPoint(bezier1, x) - BezierPoint(bezier2, y)) < 1
)
result.push_back(BezierPoint(bezier1, x));
}
return result;
}
type PointToBezier(const multiarray<vector<type>> &bezier, const vector<type> &point)
{
multiarray<vector<type>> _bezier = BezierDerivative(bezier), _bezier2 = BezierDerivative(_bezier);
auto getInterval = [](const type x) -> type
{
if(x < 0)
return 0;
if(x > 1)
return 1;
return x;
};
auto _NewtonsMethod = [&](type x)
{
x = getInterval(x);
//**********Newton's method
vector<type> d = BezierPoint<type>(bezier, x) - point, _d = BezierPoint<type>(_bezier, x);
x -= Dot(d, _d) / (Dot(d, BezierPoint<type>(_bezier2, x)) + Dot(_d, _d));
return x;
};
auto _Correction = [&](type x) -> type
{
x = getInterval(x);
//**********Correction
type head = Norm(point - bezier.front()),
middle = Norm(point - BezierPoint<type>(bezier, x)),
end = Norm(point - bezier.back());
if(middle > head && head < end)
x = 0;
if(middle > end && head > end)
x = 1;
return x;
};
return _Correction(_NewtonsMethod(_NewtonsMethod(0.5)));
}
template <typename type>
multiarray<vector<type>> &BezierIntersection(const multiarray<vector<type>> &bezier1,
const multiarray<vector<type>> &bezier2, multiarray<vector<type>> &result = multiarray<vector<type>>())
{
multiarray<vector<type>> _bezier1 = BezierDerivative(bezier1), _bezier2 = BezierDerivative(bezier2);
auto getInterval = [](const type x) -> type
{
if (x < 0)
return 0;
if (x > 1)
return 1;
return x;
};
auto _NewtonsMethod = [&](type &x, type &y)
{
x = getInterval(x);
y = getInterval(y);
//**********Newton's method
vector<type> d = BezierPoint<type>(bezier1, x) - BezierPoint<type>(bezier2, y),
_dx = BezierPoint<type>(_bezier1, x), _dy = -BezierPoint<type>(_bezier2, y);
type det = _dx[0] * _dy[1] - _dy[0] * _dx[1];
x -= (_dy[1] * d[0] - _dy[0] * d[1]) / det;
y -= (_dx[0] * d[1] - _dx[1] * d[0]) / det;
};
result.clear();
for (type i = 0; i <= 1; i += (type)1 / ((bezier1.size() - 1) * (bezier2.size() - 1)))
{
type x = PointToBezier(bezier1, BezierPoint(bezier2, i)), y = i;
_NewtonsMethod(x, y);
_NewtonsMethod(x, y);
if (x >= 0 && x <= 1 && y >= 0 && y <= 1
&& Norm(BezierPoint(bezier1, x) - BezierPoint(bezier2, y)) < 1
)
result.push_back(BezierPoint(bezier1, x));
}
return result;
}
附件 未命名.png (150.16 KB)
2014-3-9 08:13 PM
2014-3-9 08:13 PM
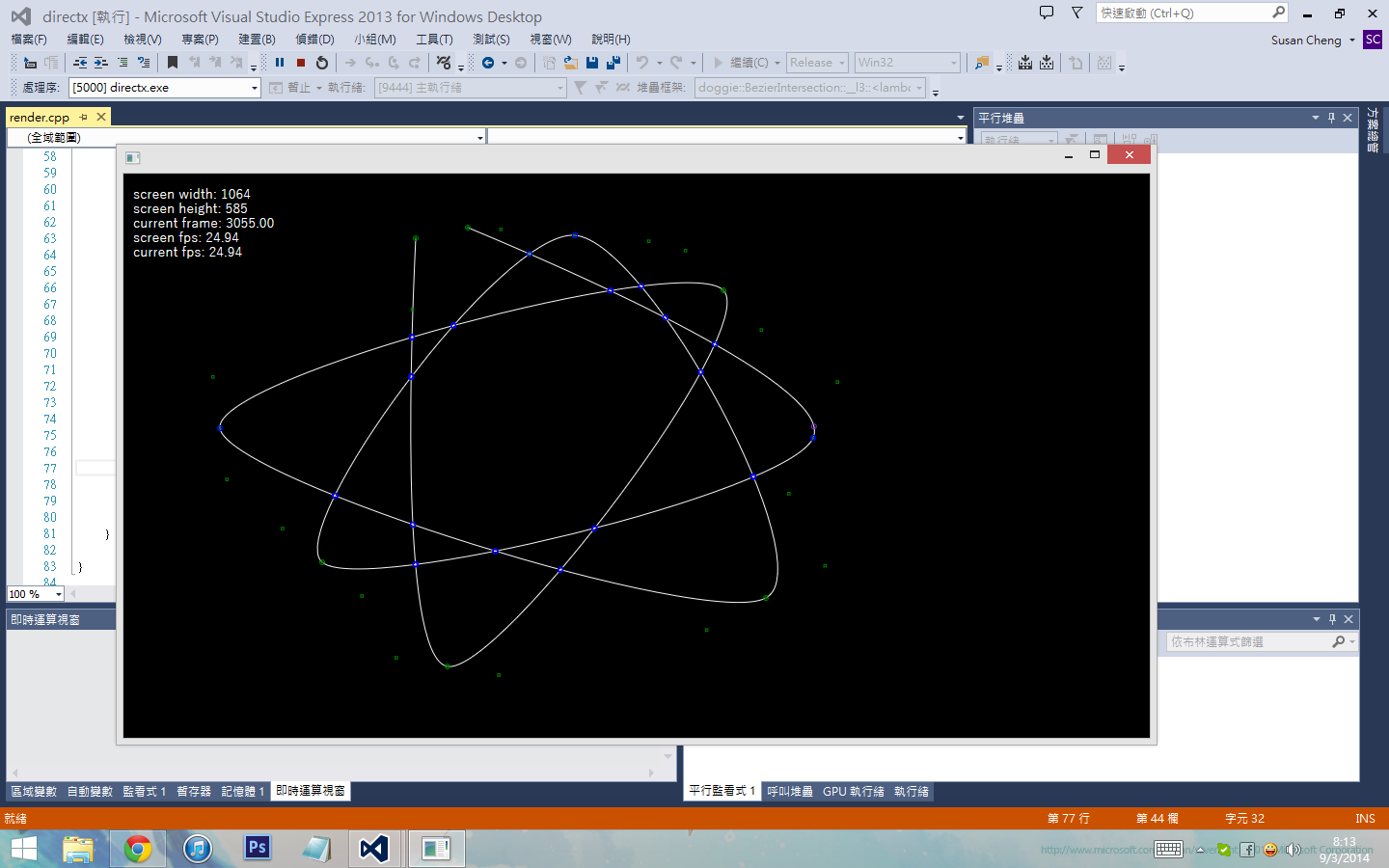
未命名.png (150.16 KB)
2014-3-9 08:13 PM

2014-3-9 08:13 PM

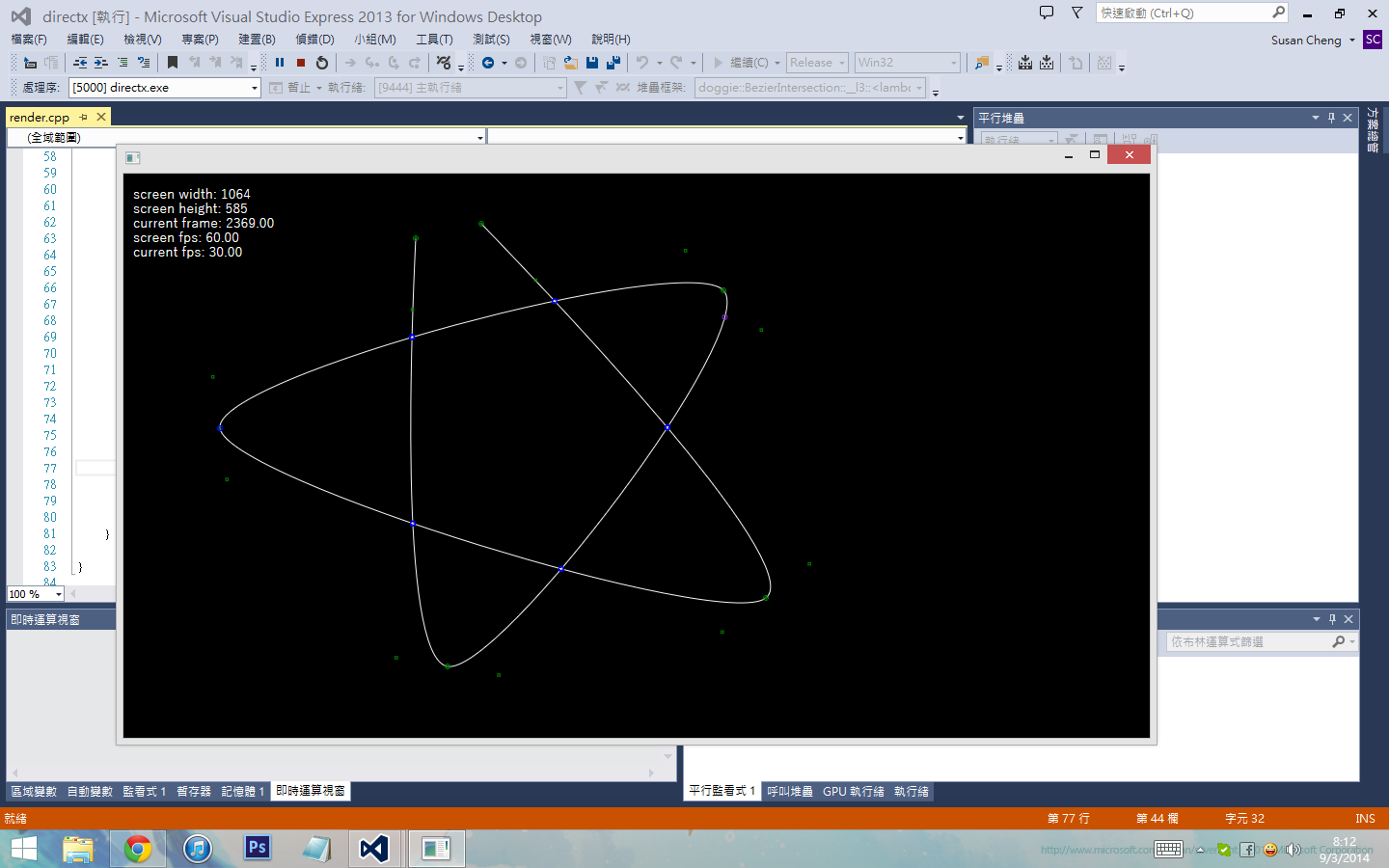
作者: Susan﹏汪汪 发布时间: 2014-03-20
个Intersection算法.....似乎bezier数量不多都影响到效能
作者: Susan﹏汪汪 发布时间: 2014-03-20
相关阅读 更多
热门阅读
-
 office 2019专业增强版最新2021版激活秘钥/序列号/激活码推荐 附激活工具
office 2019专业增强版最新2021版激活秘钥/序列号/激活码推荐 附激活工具
阅读:74
-
 如何安装mysql8.0
如何安装mysql8.0
阅读:31
-
 Word快速设置标题样式步骤详解
Word快速设置标题样式步骤详解
阅读:28
-
 20+道必知必会的Vue面试题(附答案解析)
20+道必知必会的Vue面试题(附答案解析)
阅读:37
-
 HTML如何制作表单
HTML如何制作表单
阅读:22
-
 百词斩可以改天数吗?当然可以,4个步骤轻松修改天数!
百词斩可以改天数吗?当然可以,4个步骤轻松修改天数!
阅读:31
-
 ET文件格式和XLS格式文件之间如何转化?
ET文件格式和XLS格式文件之间如何转化?
阅读:24
-
 react和vue的区别及优缺点是什么
react和vue的区别及优缺点是什么
阅读:121
-
 支付宝人脸识别如何关闭?
支付宝人脸识别如何关闭?
阅读:21
-
 腾讯微云怎么修改照片或视频备份路径?
腾讯微云怎么修改照片或视频备份路径?
阅读:28