每周编程题（22/3 - 28/3）

作者: fitcat07   发布时间: 2014-04-13

作者: Susan﹏汪汪   发布时间: 2014-04-13

作者: fitcat07   发布时间: 2014-04-13

作者: Susan﹏汪汪   发布时间: 2014-04-13

想多人参与，应该鼓励下人贴码

作者: form5   发布时间: 2014-04-13

作者: assembly.jc   发布时间: 2014-04-13

引用:原帖由 form5 於 2014-3-21 11:28 PM 发表
想多人参与，应该鼓励下人贴码

我唔知道大部分人见到解答，重会唔会参与？
如果唔会，咁咪最多只得 3 个人参与？

其实参与同贴码有必然关系吗？如有人识解，可以留名，讲下感受，对题目嘅评价之类，又或帮助未解答者，给予提示等。
我相信咁做先会更多人参与。
一星期后贴码，等解唔到嘅人参考，会唔会更好？

作者: fitcat07   发布时间: 2014-04-13

Your understanding is correct.

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 Susan﹏汪汪 於 2014-3-21 10:47 PM 发表
系手机睇错...以为佢讲一定要polygon...原来只系polyline

实作简单嘅 TSP 唔系太难，最难系每个 vertex 有 2 个选择，咁就难度大增...

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-22 09:19 AM 发表
Your understanding is correct.

Hi fitcat,

Thank you. The first problem seems not difficult, trying to solve it

作者: assembly.jc   发布时间: 2014-04-13

I just did the third one with python33, only tested with the 2 sample data given from spoj, if anyone is interested, one may take a look at http://paste.org/71326

waring : please ignore it if you dont want to read it

作者: form5   发布时间: 2014-04-13

能够解答第一题嘅网友，请尝试用你熟悉嘅第二、第三甚至第 N 语言去做。
啱啱用 Python 2.7 做完，时间系 1.99s，系 Python 语言中最慢...
最快者做到 0.84s，足足快我一倍有多...
请做到快时间嘅网友，分享下心得。

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-23 10:08 PM 发表
能够解答第一题嘅网友，请尝试用你熟悉嘅第二、第三甚至第 N 语言去做。
啱啱用 Python 2.7 做完，时间系 1.99s，系 Python 语言中最慢...
最快者做到 0.84s，足 ...

Hi fitcat,

顺利完成了第一道题，也想过用 Java 实作看看，在没有pointer 的情况下，Java处理 string 的方式是否真的不如 C 那样优雅，可惜时间有限，还是挑战完第二道题后，回头再试。

作者: assembly.jc   发布时间: 2014-04-13

第一道题目并不难，只要知道一个简单的事实，那之后便是一条直路，不需太多技巧就可到达终点，很适合初学者去做。而且，如果使用 C/C++ 去实作，还可以在解题的过程中，提升对 pointer 运用的技巧，一举二得。

另外，这道题的答案虽说是一个显然而见的事实，但我还是做了证明再实作，对其他人来说可能觉得有点多余，但过程中，感受到数学和programming 二者的结合还是一件很神奇的事，自己也乐在其中

作者: assembly.jc   发布时间: 2014-04-13

Nearest Neighbor?

引用:原帖由 form5 於 2014-3-23 19:39 发表
I just did the third one with python33, only tested with the 2 sample data given from spoj, if anyone is interested, one may take a look at http://paste.org/71326

waring : please i ...

作者: a8d7e8   发布时间: 2014-04-13

引用:原帖由 a8d7e8 於 2014-3-24 02:33 PM 发表
Nearest Neighbor?

kind of

作者: form5   发布时间: 2014-04-13

IIRC, NN won't be able to find the optimal solution for some special cases. But it offers a good starting point.

引用:原帖由 form5 於 2014-3-24 14:41 发表


kind of

作者: a8d7e8   发布时间: 2014-04-13

引用:原帖由 a8d7e8 於 2014-3-24 02:46 PM 发表
IIRC, NN won't be able to find the optimal solution for some special cases. But it offers a good starting point.

yes, extra work may be needed, something like rotating the starting entry point

作者: form5   发布时间: 2014-04-13

引用:原帖由 assembly.jc 於 2014-3-24 08:40 AM 发表
顺利完成了第一道题，也想过用 Java 实作看看，在没有pointer 的情况下，Java处理 string 的方式是否真的不如 C 那样优雅，可惜时间有限，还是挑战完第二道题后，回头再试。

系咪优雅，取决於编程者。相信不少人认为使用指标，并不优雅。

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 assembly.jc 於 2014-3-24 09:00 AM 发表
但过程中，感受到数学和programming 二者的结合还是一件很神奇的事，自己也乐在其中

编程同数学，基本上系分唔开。
数学差，编程几可肯定差。
数学好，编程多数好。
睇睇 code4food 同汪汪，两者数学都非常好，直情系好劲！因此，佢两个编程能力极佳。

作者: fitcat07   发布时间: 2014-04-13

今日做咗尐研究同测试，现在 Python 已做到 0.80s，暂时系最快。

以下列出我做第一题所用语言同时间（算法相同）：

语言 时间
C++ 0.00s
Java (SE6) 0.24s
Python 2.7 0.80s

从中可大约睇到，语言间执行效能表现嘅分别。
我会试下用 Haskell 做，希望我呢个 Haskell 初哥做得到啦...

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-24 06:43 PM 发表
系咪优雅，取决於编程者。相信不少人认为使用指标，并不优雅。

Hi fitcat,

是的。那至小对於我来说是吧。字串的分割，结合，复制全可以用加，减，等於运算子完成。快速，简洁，紧凑

作者: assembly.jc   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-24 06:49 PM 发表
编程同数学，基本上系分唔开。
数学差，编程几可肯定差。
数学好，编程多数好。
睇睇 code4food 同汪汪，两者数学都非常好，直情系好劲！因此，佢两个编程能力极佳。

Hi fitcat,

数学家 Hardy 说 98% 的数学都是没有用的。看来他的说话还是另有深意。若结合你之前所说的，看来无用的数学，不是真的没有用途，而是有如内功般隐藏於内，外显则化成其他能力表现出来。

作者: assembly.jc   发布时间: 2014-04-13

作者: Susan﹏汪汪   发布时间: 2014-04-13

作者: fitcat07   发布时间: 2014-04-13

作者: fitcat07   发布时间: 2014-04-13

作者: fitcat07   发布时间: 2014-04-13

作者: fitcat07   发布时间: 2014-04-13

作者: assembly.jc   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-26 12:14 PM 发表
我喺以下呢个帖，贴上我用 Haskell 写嘅程式码：
http://computer.discuss.com.hk/viewthread.php?tid=23091863&extra=page%3D1&frombbs=1
自知写得唔好，请熟识 Haskell 嘅网友，多多指点，感谢 ...

Hi fitcat,

Haskell 我都是初学，比唔到意见你

作者: assembly.jc   发布时间: 2014-04-13

作者: assembly.jc   发布时间: 2014-04-13

引用:原帖由 assembly.jc 於 2014-3-29 12:14 AM 发表
Haskell 我都是初学，比唔到意见你

一齐学习、讨论、研究

引用:埋首二天，终於完成了第二条，很有趣的一条题目!

㳟喜！至紧要好玩！

引用:另外，第三条是否需要某方面的知识才能解答吗? 一般人能了解吗?

照我估计，应该要用 graph theory（我提供果两条连结有相关资料）。
我谂我可以代表一般人。要了解应该唔难，但要解答到，似乎好困难。

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-29 12:16 PM 发表
一齐学习、讨论、研究㳟喜！至紧要好玩！

照我估计，应该要用 graph theory（我提供果两条连结有相关资料）。
我谂我可以代表一般人。要了解应该唔难，但要解答到，似乎好困难。

Hi fitcat,

但我睇唔明你另一个帖的程式码，估计要再学多几个月才可以交流一下心得

对! 仔细看过题目，还是可以了解它想问什么。睇返 notes，Travelling salesman problem 系 NP-complete problem. 但有算法可解 (Heuristic algorithm)，但又正如你所说，每条线有二个 end points，呢点和 TSP 唔同，问题重点就系这个地方??


另外，还有一个可地方和 TSP 不同的是，每个 end points 可以是正数或者负数，即可以是四个像限(平面上)中任何一点? TSP 只可以正数，而且是一维问题，这条问题是二维问题，需要用二点去计距离? 情况似乎比 TSP 复杂

[ 本帖最后由 assembly.jc 於 2014-3-29 02:32 PM 编辑 ]

作者: assembly.jc   发布时间: 2014-04-13

引用:原帖由 assembly.jc 於 2014-3-29 01:49 PM 发表
但我睇唔明你另一个帖的程式码，估计要再学多几个月才可以交流一下心得

你学到边度？睇紧书定系上网睇教学？斋睇学唔到喎，一定要做练习㗎。边度睇唔明？请在该帖留言讨论。

引用:对! 仔细看过题目，还是可以了解它想问什么。睇返 notes，Travelling salesman problem 系 NP-complete problem. 但有算法可解 (Heuristic algorithm)，但又正如你所说，每条线有二个 end points，呢点和 TSP 唔同，问题重点就系这个地方??

唔系必定要用 heuristic，要正解都可以，只不过唔可以有太多 vertexes。维基网有列出一个用 dynamic programming 嘅算法，我就系尝试用佢去做。无错，关键就系呢度。如果只系一条普通 TSP，果个算法已经搞掂，因为 n <= 14。

引用:另外，还有一个可地方和 TSP 不同的是，每个 end points 可以是正数或者负数，即可以是四个像限(平面上)中任何一点? TSP 只可以正数，而且是一维问题，这条问题是二维问题，需要用二点去计距离? 情况似乎比 TSP 复杂

留意我哋只须计算线嘅长度，线与线之间相连后，该线嘅长度，必定为正数。假设一题 TSP 有 3 个 vertices：A、B 同 C，我哋须要知道每个 vertex 之间距离，就会利用以下一个表：

复制内容到剪贴板代码: A B C
A 0 x01 x02
B x10 0 x12
C x20 x21 0

因为已有一个解题算法，现在只要有一个类似嘅表就做到。如只有两条线 A 同 B，每条线有两个 end points，A 同 B 就有 4 种连接方法。三条线都一样。AC、BC 都系有 4 种连接方法。个表变成：

复制内容到剪贴板代码: A B C
A 0 x0100, x0101, x0110, x0111 x0200, x0201, x0210, x0211
B x1000, x1001, x1010, x1011 0 x1200, x1201, x1210, x1211
C x2000, x2001, x2010, x2011 x2100, x2101, x2110, x2111 0

除咗个表复杂咗，喺计算过程中，须要记住空闲嘅 end points，亦增加咗好多难度。

[ 本帖最后由 fitcat07 於 2014-3-29 04:13 PM 编辑 ]

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-29 04:10 PM 发表
你学到边度？睇紧书定系上网睇教学？斋睇学唔到喎，一定要做练习㗎。边度睇唔明？请在该帖留言讨论。
唔系必定要用 heuristic，要正解都可以，只不过唔可以有太多 vertexes。维基网有列出一个用 dynamic prog ...

Hi fitcat,
我自己看书学:http://www.amazon.com/Learn-You-Haskell-Great-Good/dp/1593272839, 这本书讲解比较浅白，暂时还可以理解。

对，下面的表复杂了，只因多了一个end point。但若暂时放下，此题目和 TSP的相似性，而单纯从线段与线段之间二个 end points 去想:

假设只有二条线: L1 and L2 和 四个 end points : L1.x, L1.y 和 L2.x, L2.y，用 (x, y)去表示二点之间的距离，我们有

(L1,x, L2.x),
(L1.x, L2.y),
(L1.y, L2.x),
(L1.y, L2.y)

即 2 * 2, 四个可能性，若有三条则 2 * 2 *2, 8 种可能性，n 条线就只有 2 ^ n 个可能性。因为 n <= 14 = 16348，比较所有end points 之间的距离，还是可以在合理时间内完成。right?

另外，考虑下列二个图，若单纯只将最短距离的二点 end points 相连，可能得不到 polyline(上图) 对吗?? (究竟 polyline 定义为何??)，若下图才是正确的答案。除了考虑最短距离外，还要加多以下的条件:

一个 end point 最多只可以和另一个不同线段的 end point 相连





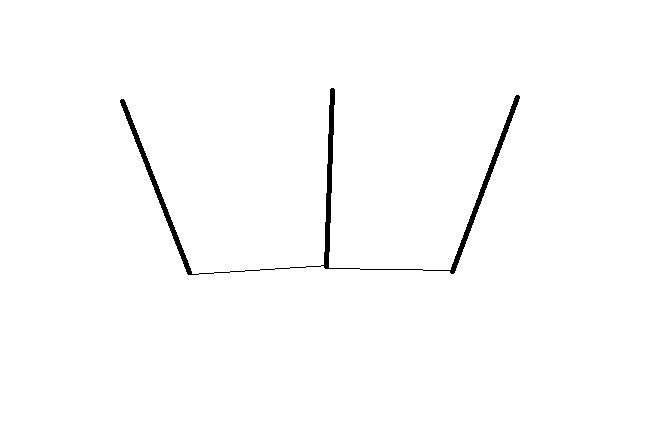
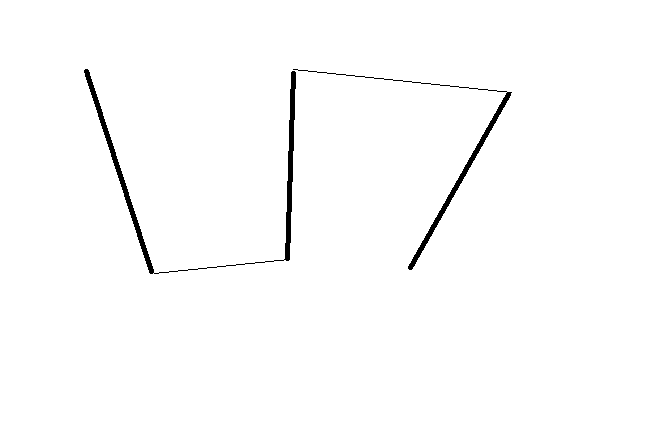
还有其他限制吗?

作者: assembly.jc   发布时间: 2014-04-13

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-3-30 01:24 PM 发表
对，呢本书讲解浅白，很易理解，初学者好啱睇，我都有睇过。但有 3 点好遗憾：1. 无练习；2. 初初睇好易明，但到后期，我完全迷失，因为久缺「点解」；3. 重有就系忽略 imperative/OO 背境嘅人。跟住我转 ...

Hi fitcat,

多谢你的意见，我想不到 Haskell 会这样难，但是目前我还是看完这本入门书再算。以后如有问题再向你讨教。

另外，之前我想说的是线段 end points 之间的连线数目，不是可能性，我词不达意，令你误会，唔好意思。和我之前的推论都是错的

看看下图

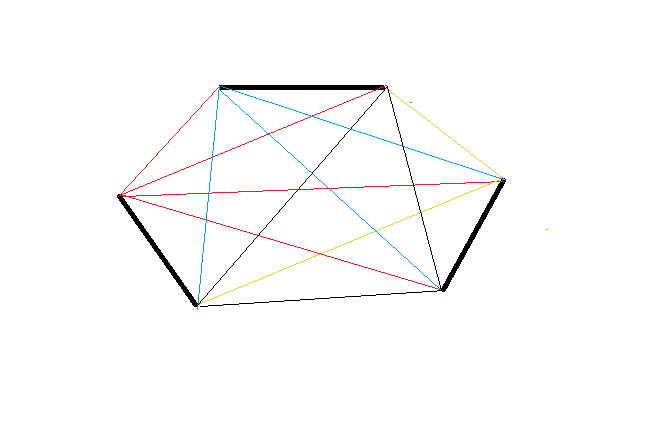
给定三条线段，end points 之间的连线是 12 条，而不是之前所说的 2^3 = 8 条，我昨日证明了一片，计算出，给定 n 条线段，end points 之间的连线数目为: (证明长了点，我放了落我的 blog里，有兴趣才去看看:)
(2n - 1)(n -1) + n -1
如 n = 14，end points 之间的连线就只有 364 条，若把所有连线的长度先排序，再由最短的连线开始，按照前一个帖所说的条件 (同一个 end points 唔可以有二条连线)，找出 13 条连线 (因给定二线段，只需一条连线，三条线段，只需二条，如此类推)，不就解决问题了吗? 还是还有其他漏洞?

[ 本帖最后由 assembly.jc 於 2014-4-9 08:39 AM 编辑 ]

作者: assembly.jc   发布时间: 2014-04-13

作者: Susan﹏汪汪   发布时间: 2014-04-13

引用:原帖由 assembly.jc 於 2014-3-31 04:30 PM 发表
多谢你的意见，我想不到 Haskell 会这样难，但是目前我还是看完这本入门书再算。以后如有问题再向你讨教。

唔好讲讨教，我都系初哥。

引用:给定三条线段，end points 之间的连线是 12 条，而不是之前所说的 2^3 = 8 条，我昨日证明了一片，计算出，给定 n 条线段，end points 之间的连线数目为: (证明长了点，我放了落我的 blog里，有兴趣才去看看:)(2n - 1)(n -1) + n -1如 n = 14，end points 之间的连线就只有 363 条，若把所有连线的长度先排序，再由最短的连线开始，按照前一个帖所说的条件 (同一个 end points 唔可以有二条连线)，找出 13 条连线 (因给定二线段，只需一条连线，三条线段，只需二条，如此类推)，不就解决问题了吗? 还是还有其他漏洞?

初步认为有道理，要再慢慢思考一下，谢谢。

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 Susan﹏汪汪 於 2014-3-31 06:47 PM 发表

呢个系会得出正确做法的答案
不过会系最没效能的方法

引用:原帖由 於 2014-3-31 10:49 PM 发表
唔好讲讨教，我都系初哥。

初步认为有道理，要再慢慢思考一下，谢谢。

Hi fitat, susan,唔好意思，之前提出的解决方法似乎并不可行。考虑下图，二图给定的线段相同，只是连结方法不同
可见，上图先连上最近的二个 end points，但结果总长度 (1 + 4.5 = 5.5) 比下图长 (2 + 2.5= 4.5)，所以之前说的先排序似乎没有作用。

但若，检视所有连线的组合，虽然最多只有364 (n=14) 条连线，但其复杂程度还是很大。以下算一算最坏情况的复杂性：
首先，考虑只有给定 2 条线段的情况，从公式 (2n - 1)(n -1) + n -1可知，end points 之间的连线数量为 4，而我们只需在 4 条连线中选一条，所以有 4 个选择。

而给定 3 条线段，end points 之间的连线数量为 12。但从 12 条连线中选取 1 条，并将 其中 2 线段连上之后，给定的 3 条线就变成了 2 条。从之前讨论可知，给定 2 条线段，有 4 个选择。所以选择总共有

12 * 4 = 48

如此类推，设 f(n) = (2n - 1)(n -1) + n -1，给定 n 条线段的复杂性是
O(f(2) * f3) * ... * f(n))

当 n = 14, 要检视所有选择似乎并不可行。问题由回到起点，唉

[ 本帖最后由 assembly.jc 於 2014-4-9 08:40 AM 编辑 ]

作者: assembly.jc   发布时间: 2014-04-13

哈哈，正想回你话排序唔可行，你已经谂到。

正在构思紧点样改 Held–Karp 算法嚟做：
http://en.wikipedia.org/wiki/Tra ... em#Exact_algorithms

作者: fitcat07   发布时间: 2014-04-13

引用:原帖由 fitcat07 於 2014-4-1 07:03 PM 发表
哈哈，正想回你话排序唔可行，你已经谂到。

正在构思紧点样改 Held–Karp 算法嚟做：
http://en.wikipedia.org/wiki/Travelling_salesman_problem#Exact_algorithms

但从线段的连线图来看，感觉像 Networks 多於 Graphs，似在 Network 中找 shortest path 的问题。而给定的线段可设为长度 0，令其一定经过，起点与终点设为同一线段，找到 shortest path 之后，会形成一条回路，之后将最长的一段连线删除，就是一条 polyline了。但有一个致命的不同，就是，选定的 end points 连线后，这二个 end points 连到其他的连线就不能再用了。

作者: assembly.jc   发布时间: 2014-04-13