当前位置：首页 → 问答吧 → 成功了

成功了

时间：2014-02-11

来源：互联网

Discrete cosine transform type II~IV, Discrete sine transform type II~IV
快速算法(全部都是使用FFT)

复制内容到剪贴板代码:template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &DCTII(const multiarray<type, Rank, Allocator> &buffer, multiarray<type, Rank, Allocator> &result)
{
typedef complex_type<type>::type complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t N = buffer.size();
multiarray<complex_type, 1, complex_alloc_type> temp(N);
for(size_t i = 0; i < N / 2; ++i)
{
temp[i] = buffer[2 * i];
temp[N - i - 1] = buffer[2 * i + 1];
}
if(N % 2)
temp[N / 2] = buffer[N - 1];
Fourier(temp, temp);
result.reshape(N);
result[0] = temp[0].real();
for(size_t i = 1; i < N; ++i)
result[i] = std::real(temp[i] * std::polar<type>((type)M_SQRT2, -(type)M_PI_2 * (type)i / (type)N));
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &DCTIII(const multiarray<type, Rank, Allocator> &buffer, multiarray<type, Rank, Allocator> &result)
{
typedef complex_type<type>::type complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t N = buffer.size();
multiarray<complex_type, 1, complex_alloc_type> temp(N);
temp[0] = (complex_type)buffer[0];
for(size_t i = 1; i < N; ++i)
temp[i] = std::polar<type>(buffer[i] * (type)M_SQRT2, -(type)M_PI_2 * (type)i / (type)N);
Fourier(temp, temp);
result.reshape(N);
for(size_t i = 0; i < N / 2; ++i)
{
result[2 * i] = temp[i].real();
result[2 * i + 1] = temp[N - i - 1].real();
}
if(N % 2)
result[N - 1] = temp[N / 2].real();
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &DCTIV(const multiarray<type, Rank, Allocator> &buffer, multiarray<type, Rank, Allocator> &result)
{
typedef complex_type<type>::type complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t N = buffer.size();
multiarray<complex_type, 1, complex_alloc_type> temp(N);
for(size_t i = 0; i < N / 2; ++i)
{
temp[i] = buffer[2 * i];
temp[N - i - 1] = -buffer[2 * i + 1];
}
if(N % 2)
temp[N / 2] = buffer[N - 1];
for(size_t i = 1; i < N; ++i)
temp[i] *= std::polar<type>(1, -(type)M_PI * (type)i / (type)N);
Fourier(temp, temp);
result.reshape(N);
for(size_t i = 0; i < N; ++i)
result[i] = std::real(temp[i] * std::polar<type>((type)M_SQRT2, -(type)M_PI_4 * (type)(2 * i + 1) / (type)N));
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &DSTII(const multiarray<type, Rank, Allocator> &buffer, multiarray<type, Rank, Allocator> &result)
{
typedef complex_type<type>::type complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t N = buffer.size();
multiarray<complex_type, 1, complex_alloc_type> temp(N);
for(size_t i = 0; i < N / 2; ++i)
{
temp[i] = -buffer[2 * i];
temp[N - i - 1] = buffer[2 * i + 1];
}
if(N % 2)
temp[N / 2] = -buffer[N - 1];
for(size_t i = 1; i < N; ++i)
temp[i] *= std::polar<type>(1, -(type)2 * (type)M_PI * (type)i / (type)N);
Fourier(temp, temp);
result.reshape(N);
for(size_t i = 0; i < N - 1; ++i)
result[i] = std::imag(temp[i] * std::polar<type>((type)M_SQRT2, -(type)M_PI_2 * (type)(i + 1) / (type)N));
result[N - 1] = std::imag(temp[N - 1] * std::polar<type>(1, -(type)M_PI_2));
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &DSTIII(const multiarray<type, Rank, Allocator> &buffer, multiarray<type, Rank, Allocator> &result)
{
typedef complex_type<type>::type complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t N = buffer.size();
multiarray<complex_type, 1, complex_alloc_type> temp(N);
for(size_t i = 0; i < N - 1; ++i)
temp[i] = std::polar<type>(buffer[i] * (type)M_SQRT2, -(type)M_PI_2 * (type)(i + 1) / (type)N);
temp[N - 1] = std::polar<type>(buffer[N - 1], -(type)M_PI_2);
Fourier(temp, temp);
for(size_t i = 1; i < N; ++i)
temp[i] *= std::polar<type>(1, -(type)2 * (type)M_PI * (type)i / (type)N);
result.reshape(N);
for(size_t i = 0; i < N / 2; ++i)
{
result[2 * i] = -temp[i].imag();
result[2 * i + 1] = temp[N - i - 1].imag();
}
if(N % 2)
result[N - 1] = -temp[N / 2].imag();
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &DSTIV(const multiarray<type, Rank, Allocator> &buffer, multiarray<type, Rank, Allocator> &result)
{
typedef complex_type<type>::type complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t N = buffer.size();
multiarray<complex_type, 1, complex_alloc_type> temp(N);
for(size_t i = 0; i < N / 2; ++i)
{
temp[i] = -buffer[2 * i];
temp[N - i - 1] = -buffer[2 * i + 1];
}
if(N % 2)
temp[N / 2] = -buffer[N - 1];
for(size_t i = 1; i < result.size(0); ++i)
temp[i] *= std::polar<type>(1, -(type)M_PI * (type)i / (type)N);
Fourier(temp, temp);
result.reshape(N);
for(size_t i = 0; i < N; ++i)
result[i] = std::imag(temp[i] * std::polar<type>((type)M_SQRT2, -(type)M_PI_4 * (type)(2 * i + 1) / (type)N));
return result;
}

作者: Susan﹏汪汪发布时间: 2014-02-11

复制内容到剪贴板代码:multiarray<double> a(GetRandom());

generate(a.begin(), a.end(), GetRandom);
show(a);
cout << endl;

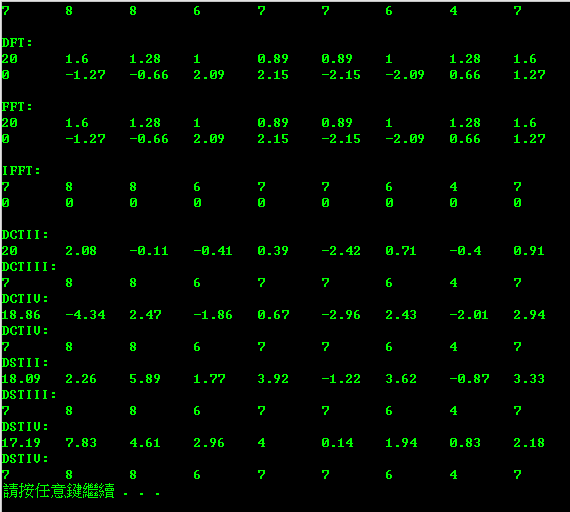
cout << "DFT: " << endl;
for(size_t i = 0; i < a.size(); ++i)
cout << round(abs(DiscreteFourier(a, i)) * 100) / 100 << '\t';
cout << endl;
for(size_t i = 0; i < a.size(); ++i)
cout << round(arg(DiscreteFourier(a, i)) * 100) / 100 << '\t';
cout << endl << endl;

cout << "FFT: " << endl;
multiarray<complex<double>> temp;
Fourier(a, temp);
for(size_t i = 0; i < temp.size(); ++i)
cout << round(abs(temp.at(i)) * 100) / 100 << '\t';
cout << endl;
for(size_t i = 0; i < temp.size(); ++i)
cout << round(arg(temp.at(i)) * 100) / 100 << '\t';
cout << endl << endl;

cout << "IFFT: " << endl;
Flip(Fourier(temp, temp), temp);
for(size_t i = 0; i < temp.size(); ++i)
cout << round(abs(temp.at(i)) * 100) / 100 << '\t';
cout << endl;
for(size_t i = 0; i < temp.size(); ++i)
cout << round(arg(temp.at(i)) * 100) / 100 << '\t';
cout << endl << endl;

cout << "DCTII: " << endl;
show(DCTII(a, a));
cout << "DCTIII: " << endl;
show(DCTIII(a, a));
cout << "DCTIV: " << endl;
show(DCTIV(a, a));
cout << "DCTIV: " << endl;
show(DCTIV(a, a));

cout << "DSTII: " << endl;
show(DSTII(a, a));
cout << "DSTIII: " << endl;
show(DSTIII(a, a));
cout << "DSTIV: " << endl;
show(DSTIV(a, a));
cout << "DSTIV: " << endl;
show(DSTIV(a, a));

附件未命名.png (11.14 KB)

2014-1-11 12:52 AM

未命名.png (11.14 KB)

2014-1-11 12:52 AM

作者: Susan﹏汪汪发布时间: 2014-02-11

虽然帮唔到你验证, 都恭喜你成功了!

作者: a8d7e8 发布时间: 2014-02-11

发现。。

DCT虽然output全部是实数
而且比较DFT多一倍频谱输出

但只可以反映到cosine的频率
不能像DFT可以反映某点的确实频率和移位

作者: Susan﹏汪汪发布时间: 2014-02-11

引用:原帖由 Susan﹏汪汪於 2014-1-12 12:03 AM 发表
发现。。

DCT虽然output全部是实数
而且比较DFT多一倍频谱输出

但只可以反映到cosine的频率
不能像DFT可以反映某点的确实频率和移位

老实说， C/C++ 程式及数学对我来说都很难明，所以我自问就无能力验证你的 code 是否正确。
不过既然你用的算法应该与网上资料一致的话，应该都没有问题。
或许可利用以下各网页中的 "Properties & Relations" 所述的特性来写 unit test ：
http://reference.wolfram.com/mathematica/ref/Fourier.html
http://reference.wolfram.com/mathematica/ref/InverseFourier.html
http://reference.wolfram.com/mathematica/ref/FourierDCT.html
http://reference.wolfram.com/mathematica/ref/FourierDST.html

作者: xianrenb 发布时间: 2014-02-11

引用:原帖由 xianrenb 於 2014-1-12 11:27 AM 发表

老实说， C/C++ 程式及数学对我来说都很难明，所以我自问就无能力验证你的 code 是否正确。
不过既然你用的算法应该与网上资料一致的话，应该都没有问题。
或许可利用以下各网页中的 "Properties & Relations" ...

汪汪上面的code是快速算法

之前试过直接运算做比对
得出结果是一样

始终对於DCTIV和DSTII~IV的资料太少
网上找不到sample

作者: Susan﹏汪汪发布时间: 2014-02-11

复制内容到剪贴板代码:multiarray<double> a(5);

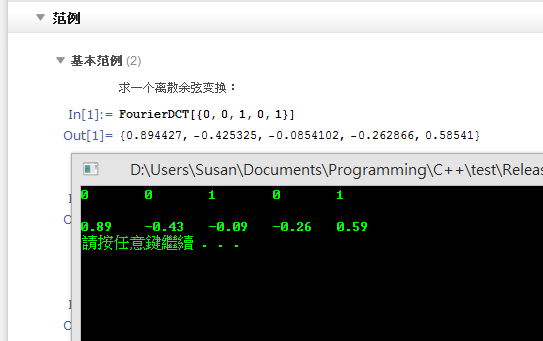
a[0] = 0;
a[1] = 0;
a[2] = 1;
a[3] = 0;
a[4] = 1;

show(a);
cout << endl;

DCTII(a, a);
for(int i = 1; i < a.size(); ++i)
a /= M_SQRT2; //取消正交性
show(a);

复制内容到剪贴板代码:multiarray<double> a(5);

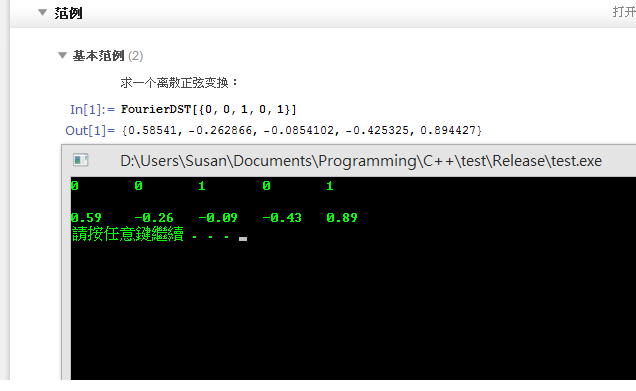
a[0] = 0;
a[1] = 0;
a[2] = 1;
a[3] = 0;
a[4] = 1;

show(a);
cout << endl;

DSTII(a, a);
for(int i = 0; i < a.size() - 1; ++i)
a /= M_SQRT2; //取消正交性
show(a);

作者: Susan﹏汪汪发布时间: 2014-02-11

除了DFT的"Properties & Relations"有实质数字

其他的如DCT只是话DCT type2和DCT type3互逆....
汪汪#2个图都是做到....先用DCT(或者DST)运算....然后再做逆运算

DCTII和DCTIII互逆
DCTIV自逆运算

DST都一样

作者: Susan﹏汪汪发布时间: 2014-02-11

http://youtu.be/TS836ufa_7U

作者: Susan﹏汪汪发布时间: 2014-02-11

引用:原帖由 Susan﹏汪汪於 2014-1-12 06:01 PM 发表
除了DFT的"Properties & Relations"有实质数字

其他的如DCT只是话DCT type2和DCT type3互逆....
汪汪#2个图都是做到....先用DCT(或者DST)运算....然后再做逆运算

DCTII和DCTIII互逆
DCTIV自逆运算

DST都一 ...

原来我忘了看这里的讨论。
或许你是以为我还在质疑你的程式。
不过以我估计你的编程能力，有错的可能性应该十分十分小。
我只是见你像在写一些 test 去测试你的程式，便建议你看一下可以利用的各种 transform 的特性来写 unit test。
大概普通人不可能用人脑直接 tranform 到不同数值的答案嘛！
所以测试都只能靠电脑依不同方法去运算来比对。
就如我们知道 x * 3 / 3 = x 。
如果我们设计了一个乘法及一个除法功能（先假设原来的电脑不能直接做），其中一个测试方法就是 random 产生 x ，然后测试 * 3 后再 / 3 的结果与原先的 x 差多少。
差得极少就可以当正确。
类似上述的过程就是自动化的 unit test 。
不知道 C++ 应该用什么写 unit test 才好。
PHP 就很可能只有 PHPUnit 。
如果有心开放程式出来给人用的话，最好把程式连 test 放在 GitHub / Google Code 一类 platform 。

作者: xianrenb 发布时间: 2014-02-11

引用:原帖由 xianrenb 於 2014-1-14 06:57 PM 发表

原来我忘了看这里的讨论。
或许你是以为我还在质疑你的程式。
不过以我估计你的编程能力，有错的可能性应该十分十分小。
我只是见你像在写一些 test 去测试你的程式，便建议你看一下可以利用的各种 transform 的 ...

不...汪汪是说...2#的code就是用你讲的方法做测试

复制内容到剪贴板代码:cout << "DCTII: " << endl;
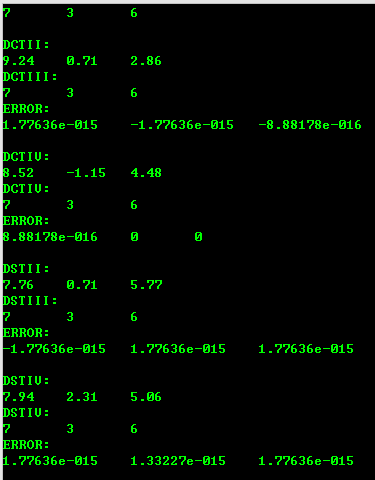
show(DCTII(a, a)); //计算DCT-II
cout << "DCTIII: " << endl;
show(DCTIII(a, a)); //利用上一行的结果...计算DCT-III...因为DCT-II和DCT-III互为逆运算...所以会还原为原signal
cout << "DCTIV: " << endl;
show(DCTIV(a, a)); //计算DCT-IV
cout << "DCTIV: " << endl;
show(DCTIV(a, a)); //利用上一行的结果...计算DCT-IV...因为DCT-IV自身为逆运算...所以会还原为原signal

基本上...上述的结果都是正常

作者: Susan﹏汪汪发布时间: 2014-02-11