convolution改进算法

事情系咁的....
因为汪汪原本写的convolution算法系使用公式:

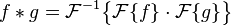
问题系...
假如有两组data
a{1, 2, 3, 4, 5, 6, 7, 8, 9}
b{1, 2}
Convolve(a, b) = {1, 4, 7, 10, 13, 16, 19, 22, 25, 18}
当然上面的公式也适用...但同时计算会很慢(应该话其实有更快的方法)

而原理系
把a分拆成{1, 2}, {3, 4}, {5, 6}, {7, 8, 9}
然后一个个咁同b做convolution
得出{1, 4, 4}, {3, 10, 8}, {5, 16, 12}, {7, 22, 25, 18}
虽然好似同目标相差太远...但只要对位做加法(点对位的话...要长篇大论了...大概系: 分段a的长度 + b的长度 - 1)

复制内容到剪贴板代码:{1, 4, 4}
{3, 10, 8}
{5, 16, 12}
{ 7, 22, 25, 18}
-------------------------------------
{1, 4, 7, 10, 13, 16, 19, 22, 25, 18}

就会得出来要的结果

而更好的消息是...第二种拆件的算法会比第一种算法快好多好多
详细唔多讲了(可以计一下复杂度的)

复制内容到剪贴板代码:template <typename arg_type, size_t Rank, typename Allocator>
multiarray<arg_type, Rank, Allocator> &_convolve(const multiarray<arg_type, Rank, Allocator> &signal,
const multiarray<arg_type, Rank, Allocator> &kernel, multiarray<arg_type, Rank, Allocator> &result)
{
using namespace std::placeholders;
typedef complex_type<arg_type>::value_type type;
typedef complex_type<arg_type>::type complex_type;
typedef std::allocator_traits<Allocator>::rebind_alloc<complex_type>::other complex_alloc_type;
size_t size[Rank], bound[Rank], N = 1;
for (size_t i = 0; i < Rank; ++i)
{
size[i] = signal.size(i) + kernel.size(i) - 1;
bound[i] = size[i] + signal.size(i) % 2 + kernel.size(i) % 2 + 1;
N *= bound[i];
}
multiarray<complex_type, Rank, complex_alloc_type> fa, fb, temp;
fa.reshape(signal.shape().begin(), signal.begin(), signal.end());
fb.reshape(kernel.shape().begin(), kernel.begin(), kernel.end());
fa.resize(bound, (complex_type)0);
fb.resize(bound, (complex_type)0);
Flip(Fourier(PointwiseProduct(Fourier(fa, fa), Fourier(fb, fb)), temp), temp);
temp.resize(size);
result.reshape(size);
__if_exists(arg_type::value_type)
{
std::transform(temp.begin(), temp.end(), result.begin(), std::bind(std::multiplies<arg_type>(), _1, std::sqrt((type)N)));
}
__if_not_exists(arg_type::value_type)
{
for (size_t i = 0; i < result.size(); ++i)
result.at(i) = temp.at(i).real();
std::transform(result.begin(), result.end(), result.begin(), std::bind(std::multiplies<arg_type>(), _1, std::sqrt((type)N)));
}
return result;
}
template <typename type, size_t Rank, typename Allocator>
multiarray<type, Rank, Allocator> &Convolve(const multiarray<type, Rank, Allocator> &signal,
const multiarray<type, Rank, Allocator> &kernel, multiarray<type, Rank, Allocator> &result)
{
size_t size[Rank], bound[Rank],
dimension = Rank, n = 0, block_size[2];
for (size_t i = 0; i < Rank; ++i)
{
bound[i] = signal.size(i);
size[i] = bound[i] + kernel.size(i) - 1;
if (i < dimension)
{
if (signal.size(i) > kernel.size(i) * 2)
{
dimension = i;
bound[i] = kernel.size(i);
block_size[0] = bound[i];
block_size[1] = bound[i];
n = signal.size(i) / kernel.size(i);
}
if (signal.size(i) * 2 < kernel.size(i)) return Convolve(kernel, signal, result);
} else if (i > dimension)
{
block_size[0] *= bound[i];
block_size[1] *= size[i];
}
}
if (dimension == Rank) return _convolve(signal, kernel, result);
multiarray<type, Rank, Allocator> temp, part;
temp.reshape(size, (type)0);
for (size_t i = 0; i < n + 1; ++i)
{
if (i == n && signal.size(dimension) % kernel.size(dimension))
bound[dimension] = signal.size(dimension) % kernel.size(dimension);
else if (i == n)
break;

part.resize(bound, (type)0);
if (dimension)
for (size_t j = 0; j < signal.size(dimension, 1); ++j)
std::copy(signal.begin() + i * block_size[0] + j * signal.size(dimension - 1, 2),
signal.begin() + i * block_size[0] + j * signal.size(dimension - 1, 2) + part.size(dimension - 1, 2),
part.begin() + j * part.size(dimension - 1, 2));
else
std::copy(signal.begin() + i * block_size[0], signal.begin() + i * block_size[0] + part.size(), part.begin());
Convolve(part, kernel, part);
if (dimension)
for (size_t j = 0; j < part.size(dimension, 1); ++j)
std::transform(part.begin() + j * part.size(dimension - 1, 2),
part.begin() + (j + 1) * part.size(dimension - 1, 2),
temp.begin() + i * block_size[1] + j * temp.size(dimension - 1, 2),
temp.begin() + i * block_size[1] + j * temp.size(dimension - 1, 2), std::plus<type>());
else
std::transform(part.begin(), part.end(), temp.begin() + i * block_size[1], temp.begin() + i * block_size[1], std::plus<type>());
}

return result = temp;
}

[ 本帖最后由 Susan﹏汪汪於 2014-3-14 01:26 AM 编辑 ]

作者: Susan﹏汪汪发布时间: 2014-03-24

Overlap add method?

作者: a8d7e8 发布时间: 2014-03-24

引用:原帖由 a8d7e8 於 2014-3-14 03:21 AM 发表
Overlap add method?

系

作者: Susan﹏汪汪发布时间: 2014-03-24

点解我既 program 显示出无分别既......

复制内容到剪贴板代码:operations: 18
[1, 4, 7, 10, 13, 16, 19, 22, 25, 18]
operations: 4
[1, 4, 4]
operations: 4
[3, 10, 8]
operations: 4
[5, 16, 12]
operations: 6
[7, 22, 25, 18]

复制内容到剪贴板代码: for k in xrange(xh + xn - 1):
rez.append(0)
for j in xrange(xh):
if 0 <= k-j < xn:
rez[k] = rez[k] + (h[j] * x[k-j]);
cnt = cnt + 1;

作者: a8d7e8 发布时间: 2014-03-24

引用:原帖由 a8d7e8 於 2014-3-14 04:13 AM 发表
点解我既 program 显示出无分别既......

operations: 18
[1, 4, 7, 10, 13, 16, 19, 22, 25, 18]
operations: 4
[1, 4, 4]
operations: 4
[3, 10, 8]
operations: 4
[5, 16, 12]
operations: 6
[7, ...

因为你做的convolution不是用FFT
拆件计算和直接计算同样系O(MN)的复杂度

但如果用FFT去做的话
因为两组data的长度相差唔多的话、效率系最好

作者: Susan﹏汪汪发布时间: 2014-03-24

FFT的convolution算法系O( (M+N-1)*log(M+N-1) )

而如果拆件的话
M=kN
复杂度变成O( k*(2N-1)*log(2N-1) )

当然、如果拆件太多的话
其实就变成直接计算
M=Kp (p接近1)
复杂度就是直接计算的复杂度O( K*(N+p-1)*log(N+p-1) ) 接近 O( M*(N)*log(N) )
当中的log(N)就是FFT的额外开销

作者: Susan﹏汪汪发布时间: 2014-03-24

哦! 你用 discrete number 来说明在 FFT 算法下的优化概念.

咁用 FFT 计即系点啊?

有无 sample input and output? 我想试下用 scilab 计.

引用:原帖由 Susan﹏汪汪於 2014-3-14 11:52 发表

因为你做的convolution不是用FFT
拆件计算和直接计算同样系O(MN)的复杂度

但如果用FFT去做的话
因为两组data的长度相差唔多的话、效率系最好

作者: a8d7e8 发布时间: 2014-03-24

汪汪无sample

可以试试
a: 5000个乱数
b: 100个乱数

用FFT版convolution计一次结果并计时
再用拆件版再计一次、比对结果

作者: Susan﹏汪汪发布时间: 2014-03-24

还是 input 同 output 一样，只系计算过程有无转去 freq domain?

哦。。。。。。似乎 kernel size 大在 freq domain 会快过在 time domain.

好似有返啲印象了。。。。。

但如果为咗加速 freq domain 而减细 kernel size, 岂不在 time domain 计算更快?

引用:原帖由 a8d7e8 於 2014-3-14 13:08 发表
哦! 你用 discrete number 来说明在 FFT 算法下的优化概念.

咁用 FFT 计即系点啊?

有无 sample input and output? 我想试下用 scilab 计.

作者: a8d7e8 发布时间: 2014-03-24

汪汪段code有两个function
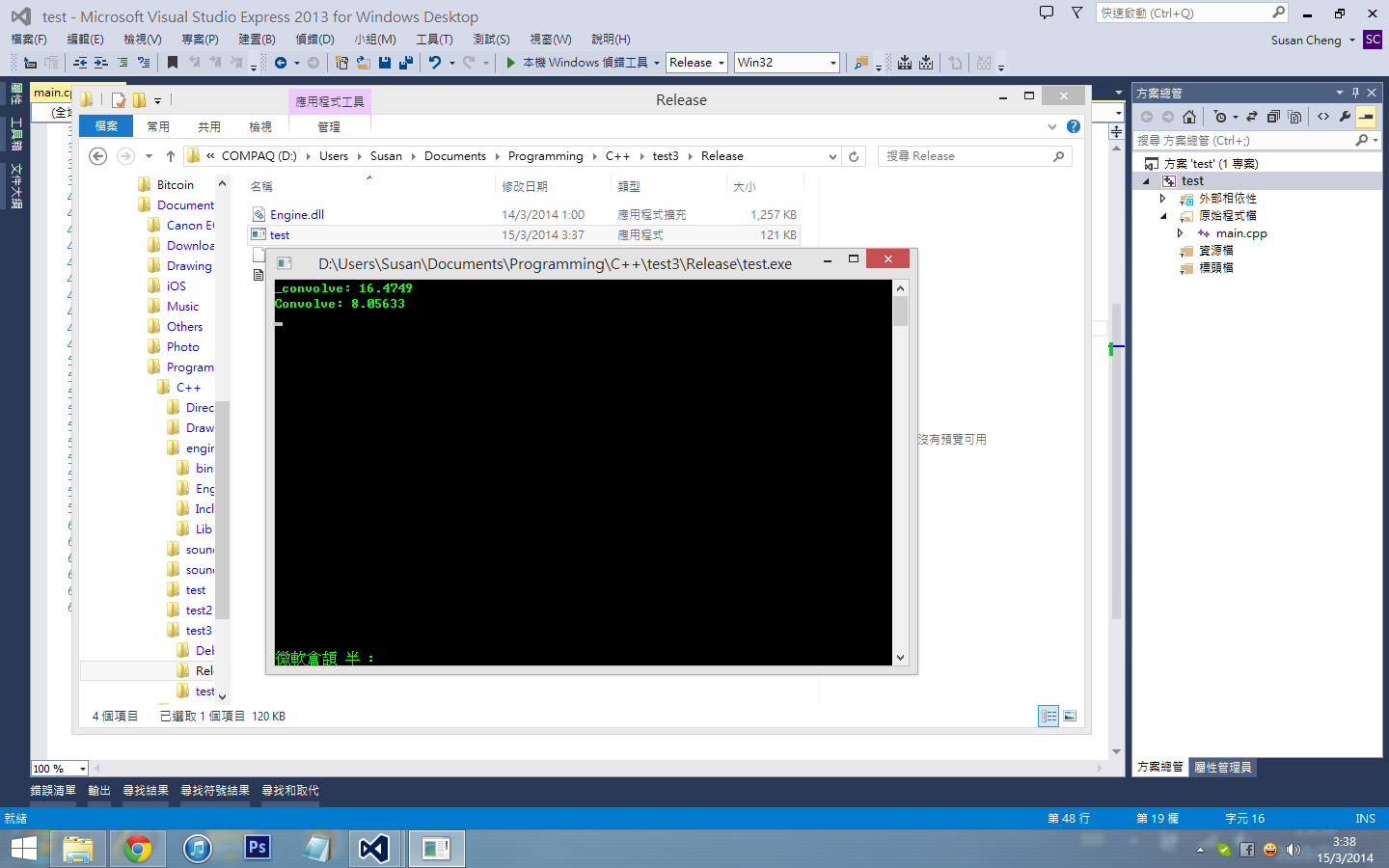
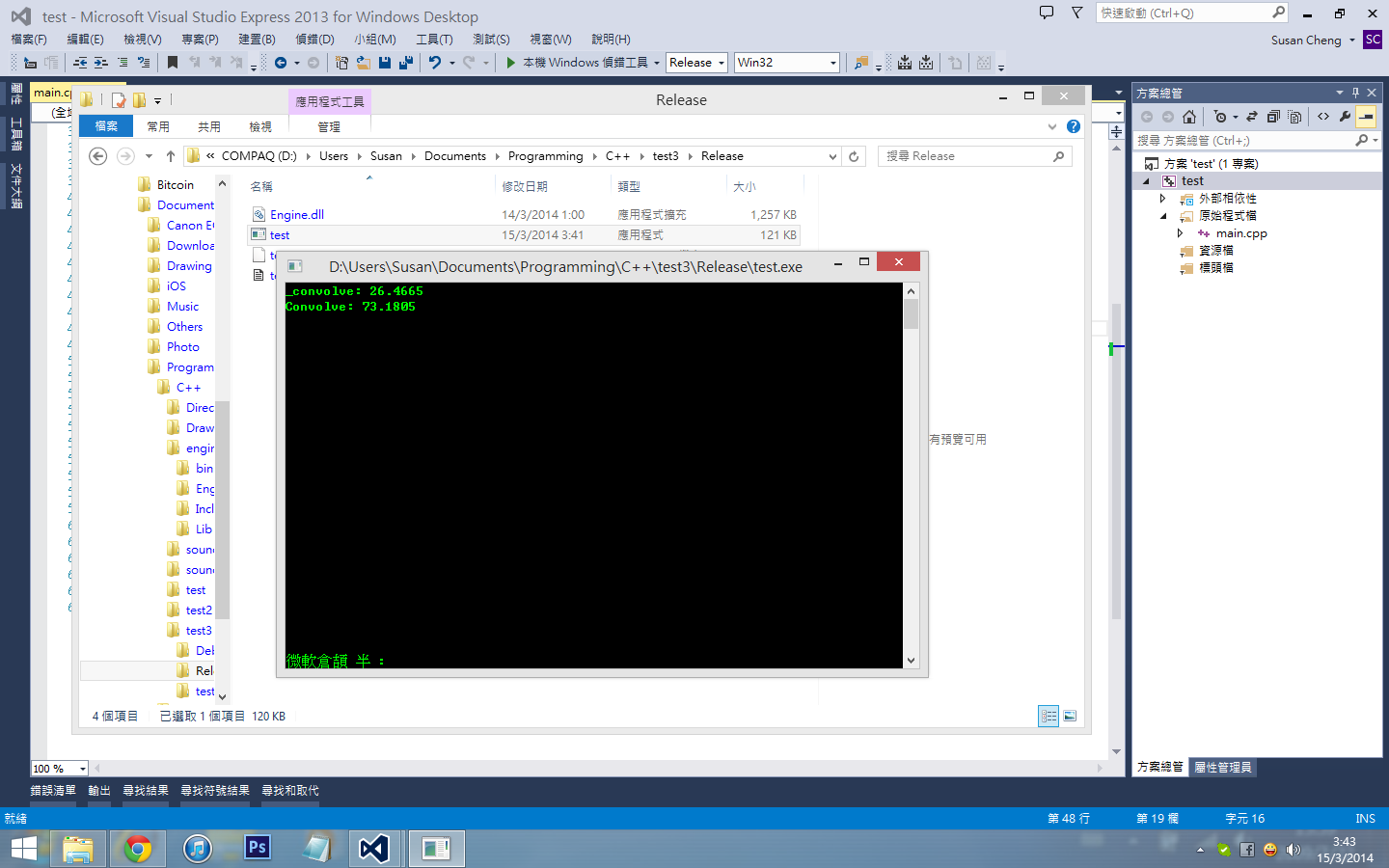
_convolve系直接FFT计算convolution
Convolve系拆件function、里面都会call _convolve function

之前试过计时
在计算两组data
a系6*6的2D array
b系2*2的2D array
使用Convolve会比较直接使用_convolve快24倍

作者: Susan﹏汪汪发布时间: 2014-03-24

引用:原帖由 Susan﹏汪汪於 2014-3-14 01:24 AM 发表
事情系咁的....
因为汪汪原本写的convolution算法系使用公式:3182120

问题系...
假如有两组data
a{1, 2, 3, 4, 5, 6, 7, 8, 9}
b{1, 2}
Convolve(a, b) = {1, 4, 7, 10, 13, 16, 19, 22, 25, 18}
当然上面的 ...

见到那样复杂的 C++ template ，我自问真的跟不上，投降了！
加上数学上要理解都不易，帮不上忙。

作者: xianrenb 发布时间: 2014-03-24

引用:原帖由 xianrenb 於 2014-3-14 01:35 PM 发表

见到那样复杂的 C++ template ，我自问真的跟不上，投降了！
加上数学上要理解都不易，帮不上忙。

因为汪汪写的系任意维的array
可以是1D、2D、3D等等
砌出来的模板就会好复杂

不过因为使用的系parallel算法
所以如果用parallel堆看的话、一层层的recursive混合开枝散叶的parallel
都会变得好壮观（而且debug会更呕血）

作者: Susan﹏汪汪发布时间: 2014-03-24

汪汪可否教教我怎样在 matlab / scilab 用 fft 计 convolution 啊?

我找到 .* 系 point-wise multiplication (dot product?)

找到 fft() 做 fft, ifft() 做 inverse fft, 但不知道 convolution 嗰个 asterisk 符号要点做...

引用:原帖由 Susan﹏汪汪於 2014-3-14 13:16 发表
汪汪段code有两个function
_convolve系直接FFT计算convolution
Convolve系拆件function、里面都会call _convolve function

之前试过计时
在计算两组data
a系6*6的2D array
b系2*2的2D array
使用Convolve会比较直接 ...

作者: a8d7e8 发布时间: 2014-03-24

引用:原帖由 a8d7e8 於 2014-3-14 01:49 PM 发表
汪汪可否教教我怎样在 matlab / scilab 用 fft 计 convolution 啊?

我找到 .* 系 point-wise multiplication (dot product?)

找到 fft() 做 fft, ifft() 做 inverse fft, 但不知道 convolution 嗰个 ast ...

a同b都要先做zero pudding
长度最少系a.size + b.size - 1
Convolve( a, b ) = ifft( fft( a ) .* fft( b ) )

作者: Susan﹏汪汪发布时间: 2014-03-24

Zero pudding的freq会有所改变

但做完asterisk并做埋ifft
Zero pudding完全不影响结果、因为数学上zero pudding的convolution系等价的

作者: Susan﹏汪汪发布时间: 2014-03-24

修正:

有两输入, a 同 b. 一般称细啲嗰个为 kernel. 所以 overlap-add method 的重点在於把 data 缩细至和 kernel size 一样或接近, 来降低做在 fft 计 convolution 的成本.

由於 kernel size 大过 10 (根据 http://stackoverflow.com/questio ... olution-calculation 的 8Nlog2N <= 2N^2) 用 freq domain 计个 time complexity 低啲, 所以不存在"为咗加速而减细 kernel size", 因为 kernel size 不变, 变的是 data size....
不过当中在 fft 怎计算 convolution 不太清楚, 要验证我既思想正确不就要等待进一步资料....

引用:原帖由 a8d7e8 於 2014-3-14 13:15 发表
还是 input 同 output 一样，只系计算过程有无转去 freq domain?

哦。。。。。。似乎 kernel size 大在 freq domain 会快过在 time domain.

好似有返啲印象了。。。。。

但如果为咗加速 freq d ...

作者: a8d7e8 发布时间: 2014-03-24

哦原来系咁做! 难怪我初步计个 size 差啲 .

同埋睇多次你对 fft convolution 个定义系不用理会 asterisk 喎!! 用 fft, ifft 同 .* 已经得, wow !

我睇 wiki http://en.wikipedia.org/wiki/Convolution_theorem 睇到第一第二条式想验证下所以 kick 住喺 asterisk 系乜度. 原来 asterisk 个 convolution 系等於 time domain 的 O(MN) function............太耐无用脑傻咗添!!

宜家我搵紧方法做 zero padding.

引用:原帖由 Susan﹏汪汪於 2014-3-14 13:56 发表
Zero pudding的freq会有所改变

但做完asterisk并做埋ifft
Zero pudding完全不影响结果、因为数学上zero pudding的convolution系等价的

作者: a8d7e8 发布时间: 2014-03-24

Oh yes!

a=[1:9];
b=[1:2];
na = length(a);
nb = length(b);
a(na+nb-1) = 0;
b(na+nb-1) = 0;
ifft(fft(a).*fft(b))

ans =
1. 4. 7. 10. 13. 16. 19. 22. 25. 18.

谢汪汪!

作者: a8d7e8 发布时间: 2014-03-24

引用:原帖由 a8d7e8 於 2014-3-14 02:08 PM 发表
哦原来系咁做! 难怪我初步计个 size 差啲 .

同埋睇多次你对 fft convolution 个定义系不用理会 asterisk 喎!! 用 fft, ifft 同 .* 已经得, wow !

我睇 wiki http://en.wikipedia.org/wiki/Convolution_t ...

其实汪汪都不清楚咩野系asterisk
总之就是point-wise multiplication
但不是dot product

作者: Susan﹏汪汪发布时间: 2014-03-24

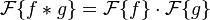
噢我讲得唔好, asterisk 系指 convolution 嗰个 symbol..

asterisk 就系左手边嗰个 *, point-wise multiplication 系右手边嗰个 ".".

丫 dot product 好似系计返一个 magnitude 数出来. OvO 太耐无用唔记得晒, sorry!!

引用:原帖由 Susan﹏汪汪於 2014-3-14 14:16 发表

其实汪汪都不清楚咩野系asterisk
总之就是point-wise multiplication
但不是dot product

作者: a8d7e8 发布时间: 2014-03-24

引用:原帖由 a8d7e8 於 2014-3-14 02:21 PM 发表
噢我讲得唔好, asterisk 系指 convolution 嗰个 symbol..

http://upload.wikimedia.org/math/4/a/6/4a6b091608e53abcb729d21f918203fb.png

asterisk 就系左手边嗰个 *, point-wise multiplication ...

原来如此

作者: Susan﹏汪汪发布时间: 2014-03-24

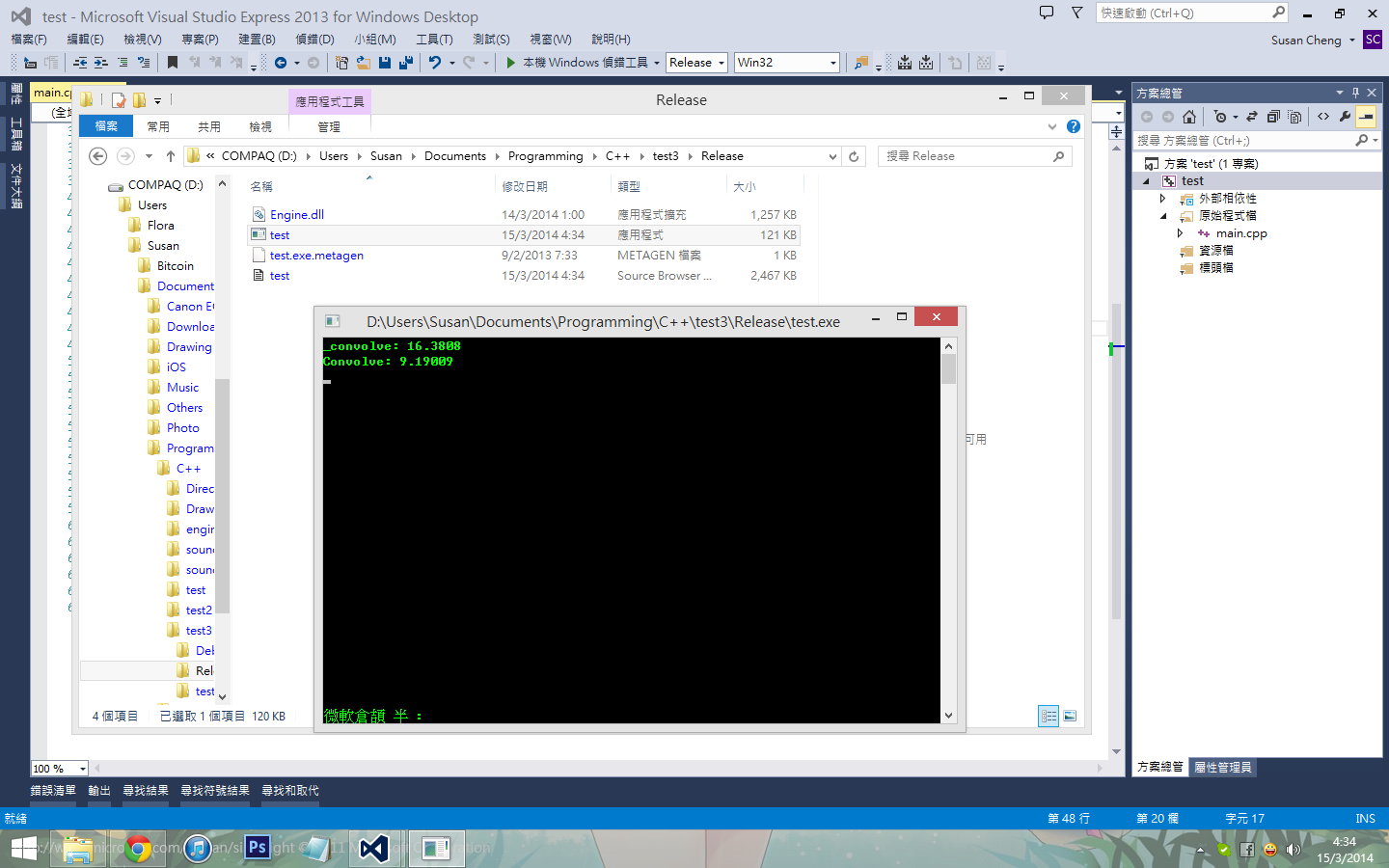
汪汪发现.....overlap-add method的效能....在决定每块block的大小会有好大影响
有时会有更好的效能...也有时会有过份的效能

附件未命名.png (145.7 KB)

2014-3-15 03:44 PM

未命名2.png (145.76 KB)

2014-3-15 03:44 PM

未命名.png (145.7 KB)

2014-3-15 03:44 PM

未命名2.png (145.76 KB)

2014-3-15 03:44 PM

作者: Susan﹏汪汪发布时间: 2014-03-24

继续做调整

附件未命名.png (189.75 KB)

2014-3-15 04:35 PM

未命名.png (189.75 KB)

2014-3-15 04:35 PM

作者: Susan﹏汪汪发布时间: 2014-03-24

汪汪plot了图
http://www.wolframalpha.com/input/?i=plot+y%28x%2Bc-1%29%28log%28x%2Bc-1%29%2B1%29-%28xy%2Bc-1%29%28log%28xy%2Bc-1%29%2B1%29%2Cx%3D0..1000%2Cy%3D0..1000%2Cc%3D10
http://www.wolframalpha.com/input/?i=plot+y%28x%2Bc-1%29%28log%28x%2Bc-1%29%2B1%29-%28xy%2Bc-1%29%28log%28xy%2Bc-1%29%2B1%29%2Cx%3D0..20%2Cy%3D0..20%2Cc%3D10
http://www.wolframalpha.com/input/?i=plot+y%28x%2Bc-1%29%28log%28x%2Bc-1%29%2B1%29-%28xy%2Bc-1%29%28log%28xy%2Bc-1%29%2B1%29%2Cx%3D0..10%2Cy%3D0..10%2Cc%3D10

又做了一些试验...多数情况系
如果把signal分成sqrt(signal.size)咁多份....通常情况都不错

作者: Susan﹏汪汪发布时间: 2014-03-24

引用:原帖由 Susan﹏汪汪於 2014-3-15 05:32 PM 发表
汪汪plot了图
http://www.wolframalpha.com/input/?i=plot+y%28x%2Bc-1%29%28log%28x%2Bc-1%29%2B1%29-%28xy%2Bc-1%29%28log%28xy%2Bc-1%29%2B1%29%2Cx%3D0..1000%2Cy%3D0..1000%2Cc%3D10
http://www.wolframalpha ...

我明少少又唔系好明你开首想说的方法。
不过我知 FFT 应该当 size = 2^n 可用最容易、最有效率的方法做。
而 convolution 可利用 FFT 来做。
那么有没有可能每段 data block 都变成 size = 2^m 、 2^n …… ，再把（可能不同 size 的）data block 合拼？

作者: xianrenb 发布时间: 2014-03-24

引用:原帖由 xianrenb 於 2014-3-16 08:55 AM 发表

我明少少又唔系好明你开首想说的方法。
不过我知 FFT 应该当 size = 2^n 可用最容易、最有效率的方法做。
而 convolution 可利用 FFT 来做。
那么有没有可能每段 data block 都变成 size = 2^m 、 2^n …… ，再 ...

FFT的效率浪费在把data resize
尤其把两组大小相差太大的data

汪汪还在研究各种情况下的最优算法

作者: Susan﹏汪汪发布时间: 2014-03-24

引用:原帖由 Susan﹏汪汪於 2014-3-16 01:27 PM 发表

FFT的效率浪费在把data resize
尤其把两组大小相差太大的data

汪汪还在研究各种情况下的最优算法

我的意思是指例如把 {1,2,3,...,13} 分拆成 {1,2,3,...,8}, {9,10,11,12} 及 {13} 来分别做 convolution，完成后再加起来。
因为按你开首说的意思，应该分开计算后再合并可以增加效率，所以我才有这个想法。
问题的 size 就由 13 转成 8 、 4 及 1 ，应该都是 FFT 最有效率的 size 。
断估时间以 big o notation 来算，应该没有增加吧？

作者: xianrenb 发布时间: 2014-03-24

引用:原帖由 xianrenb 於 2014-3-17 01:53 PM 发表

我的意思是指例如把 {1,2,3,...,13} 分拆成 {1,2,3,...,8}, {9,10,11,12} 及 {13} 来分别做 convolution，完成后再加起来。
因为按你开首说的意思，应该分开计算后再合并可以增加效率，所以我才有这个想法。
问题 ...

又系wor

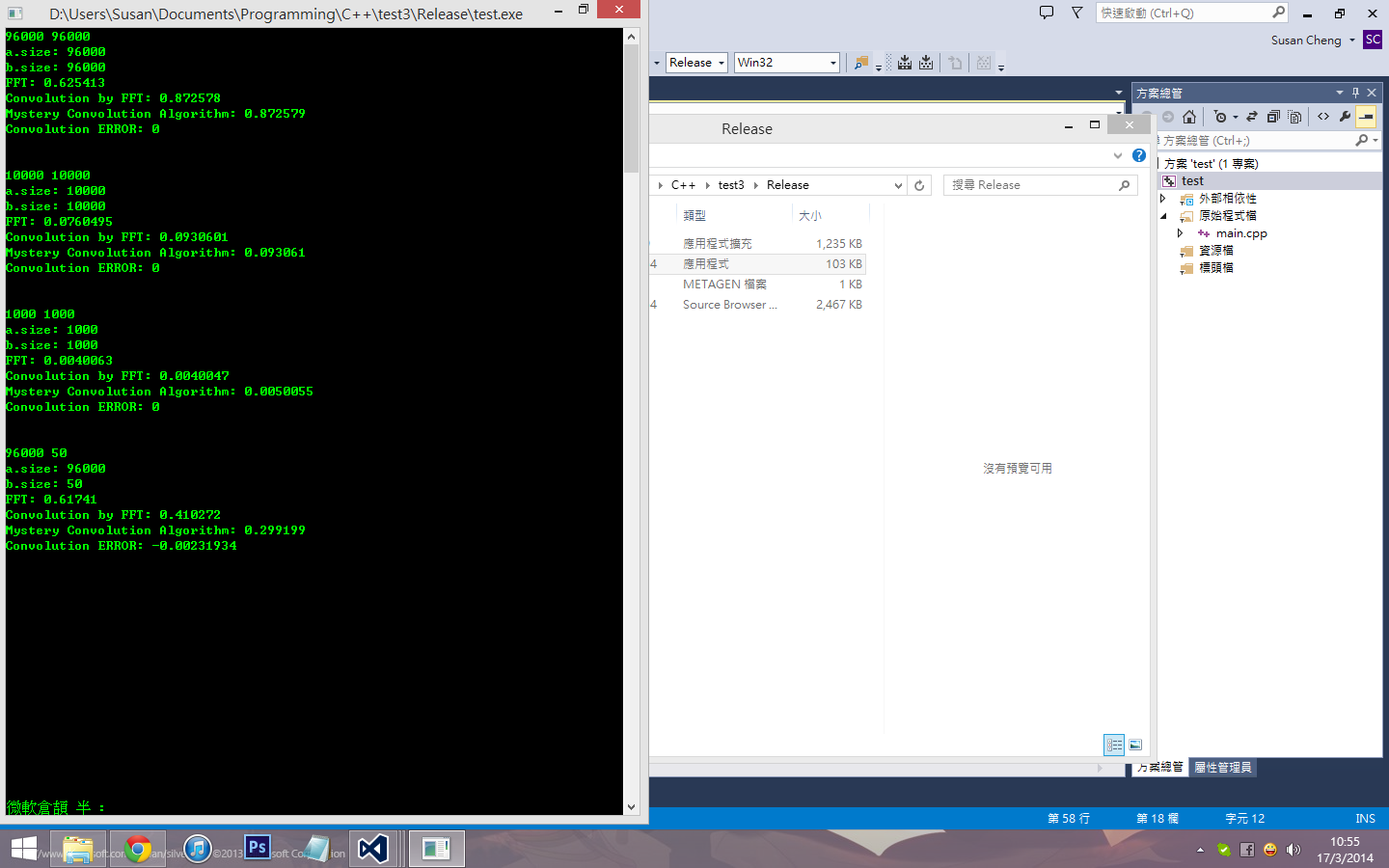
不过效能上未必有明显提升

因为convolution by fft
本身要把a和b的data同时做zero pudding最少至a.size + b.size - 1

[ 本帖最后由 Susan﹏汪汪於 2014-3-17 02:01 PM 使用编辑 ]

作者: Susan﹏汪汪发布时间: 2014-03-24

结果就是
Signal就算系分割成2^n size
Kernel 未必会系2^n size

同埋到最后做zero pudding一样不会理输入的data系咪2^n size

作者: Susan﹏汪汪发布时间: 2014-03-24

引用:原帖由 Susan﹏汪汪於 2014-3-17 02:04 PM 发表
结果就是
Signal就算系分割成2^n size
Kernel 未必会系2^n size

同埋到最后做zero pudding一样不会理输入的data系咪2^n size

如果 signal 分割成 2^n size 有可能提升效能的话， kernel 亦应该可以作相同的分割方式。
情况就有可能像计算两个百位数相乘时（abc * def），可分别计算 a*d 、 a*e 、 a*f 、 b*d 、 b*e 、 b*f 、 c*d 、 c*e 、 c*f ，然后再对位后把所有结果加起来。
不过我都只是估下，不知实际上是否 ok 。

[ 本帖最后由 xianrenb 於 2014-3-17 06:22 PM 编辑 ]

作者: xianrenb 发布时间: 2014-03-24

引用:原帖由 xianrenb 於 2014-3-17 06:20 PM 发表

如果 signal 分割成 2^n size 有可能提升效能的话， kernel 亦应该可以作相同的分割方式。
情况就有可能像计算两个百位数相乘时（abc * def），可分别计算 a*d 、 a*e 、 a*f 、 b*d 、 b*e 、 b*f 、 c*d 、 c*e ...

试试先
因为如果以2^n size做分割、似乎做zero pudding的话都不会变成太长的data

作者: Susan﹏汪汪发布时间: 2014-03-24

做了实验....改用2^n size反而更糟